Após ouvir falar superficialmente sobre comitês de algoritmos de clusterização [1], me perguntei: qual seria um jeito esperto de agregar as decisões individuais de cada um dos clusters em um valor final? A resposta não é imediata, principalmente porque o problema aqui é que a definição de cada cluster pode ser diferente mesmo quando eles concordam nas separações.
Por exemplo, dado um conjunto de oito exemplos, as segmentações
[0, 0, 1, 0, 2, 2, 2, 1] e [1, 1, 0, 1, 3, 3, 3, 0] são idênticas a menos de uma permutação de nomes, isto é, basta chamar o cluster 0 de 1 e o 1 de 0 em alguma das listas e o 3 de 2 na segunda lista (ou o 2 de 3 na primeira lista). É importante ter clareza de que esses clusters de fato concordam, uma vez que a nomenclatura não tem significado algum já que não estamos num problema de classificação.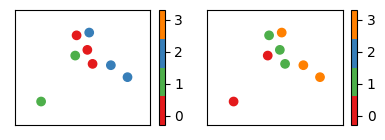
Isso motiva a criação de métricas de "avaliação de clusterização" como a
sklearn.metrics.rand_score que responde a pergunta: o quão similar são duas clusterizações? Em que, obter o valor próximo de 1 significa que os agrupamentos concordam bastante (a menos de possíveis trocas de nomes).from sklearn.metrics import rand_score
rand_score([0, 0, 1, 0, 2, 2, 2, 1], [1, 1, 0, 1, 3, 3, 3, 0])
1.0
$\oint$ A ideia por trás do (unadjusted) rand index é bem intuitiva e para explicar, vamos pensar em um exemplo específico. Imagine o cenário em que temos um conjunto de dados
[a, b, c, d] e duas clusterizações possíveis: A = [1, 1, 0, 0] e B = [1, 1, 1, 2].- Primeiro, separamos todos os pares possíveis de elementos que temos no nosso conjunto. No nosso exemplo teríamos
(a, b),(a, c),(a, d),(b, c),(b, d)e(c, d). - Em seguida, contabilizamos quantos desses pares concordam nas clusterizações
AeB. Concordar nas clusterizações significa que estão no mesmo cluster ao mesmo tempo, tanto emAquanto emB, ou não estão no mesmo cluster ao mesmo tempo nas duas clusterizações. No nosso caso, o par(a, b)concorda porque, tanto emAquanto emB, ambos estão no mesmo cluster. Mas também os pares(a, d)e(b, d)concordam nas duas clusterizações porque são alocados em clusters diferentes simultaneamente. - Com o número de pares concordantes, fazemos a razão pelo número total de pares para ter o valor do unadjusted rand index calculado, nossa medida de similaridade entre agrupamentos. No nosso caso,
3/6=0.5.
rand_score([1, 1, 0, 0], [1, 1, 1, 2])
0.5
Essas permutações deixam o problema extremamente mais desafiador do que temos num comitê supervisionado e existe uma literatura extensa [1] que tenta abordá-lo uma vez que gostaríamos de poder utilizar ideias de comitê também aqui.
Conversando com o Alessandro, tentamos encarar esse problema em uma versão mais compacta dele, analisando o caso específico de comitê de
sklearn.cluster.KMeans (apesar de mais simples, ainda assim seria um caso com possível ganho prático pela popularidade do método). A hipótese seria de que é possível utilizar os centróides para achar as concordâncias entre os diferentes estimadores individuais e daí surgiu a ideia de clusterizar os centróides dos sklearn.cluster.KMeans individuais para renomear os clusters finais de uma maneira única entre os diferentes estimadores individuais.Para exemplificar a ideia, um exemplo ajuda: se temos dois
sklearn.cluster.KMeans com n_clusters=3, então teríamos três centróides $K_1, K_2, K_3$ associados ao primeiro sklearn.cluster.KMeans e os centróides $C_1, C_2, C_3$ do segundo sklearn.cluster.KMeans. Se, ao clusterizar (com o mesmo número de clusters n_clusters), encontrássemos os metaclusters $G_1 = \{ K_1, C_1 \}$, $G_2 = \{ K_2, K_3, C_3\}$ e $G_3 = \{ C_2\}$, então teríamos um mapeamento na hora de agregar o resultado dos diferentes sklearn.cluster.KMeans individuais.Um exemplo que cai no cluster do centróide $K_1$ no primeiro agrupamento e no de $C_3$ no segundo é associado ao cluster $G_1$ com peso $1/2=0.5$ (já que um de dois K-Means base associou-o a esse grupo), ao cluster $G_2$ com peso $1/2=0.5$ (já que um de dois K-Means base associou-o a esse grupo) e ao cluster $G_3$ com peso $0/2=0$ (já que nenhum dos dois K-Means base associou-o a esse grupo). Já um exemplo que cai em $K_3$ e $C_3$ nos agrupamentos individuais estaria associado ao grupo $G_2$ com peso $2/2=1$, enquanto nos outros $G_i$ com peso $0$. Outros casos são análogos. Nesse formato, estamos voltando à mesma ideia de uma votação de um comitê clássico de classificação para criar um índice de pertencimento de cada exemplo em cada cluster como um algoritmo de soft clustering.
Testando a ideia no dataset de dígitos
Para fazer um experimento com esse modelo, vamos brincar com o conjunto de imagens de baixa resolução de dígitos escritos à mão que podemos carregar usando a função
sklearn.datasets.load_digits.from sklearn.datasets import load_digits
digits = load_digits(n_class=9)
X = digits.data
X.shape
(1617, 64)
Para introduzir variância nos clusters individuais e eles não concordarem totalmente (a menos de alguma permutação), podemos tanto mudar a estratégia de treinamento do
sklearn.cluster.KMeans (por exemplo, diminuindo o número de inicializações que ele faz para encontrar a melhor partição em termos de inércia), quanto fazer um bootstrap do nosso conjunto de treino (inspirado em como um bagging funciona no caso supervisionado). Nesse experimento, estamos seguindo com a segunda opção.from sklearn.cluster import KMeans
n_estimators = 250
n_clusters = 9
km_list = \
[KMeans(n_clusters=n_clusters, random_state=i)
.fit(X[np.random.RandomState(i).choice(X.shape[0], X.shape[0])])
for i in tqdm(range(n_estimators))]
Após treinar os diferentes
sklearn.cluster.KMeans, precisamos treinar o "Meta K-Means" que utilizará os centróides para treinamento.cluster_centers = np.vstack([km.cluster_centers_ for km in km_list])
meta_kmeans = KMeans(n_clusters=n_clusters, random_state=42).fit(cluster_centers)
Desse modo, conseguimos construir os mapeamentos que agrupam os centróides fazendo a tradução dos clusters individuais de forma que eles concordem de acordo com o critério de agrupamento do "Meta K-Means".
meta_clusters_map = \
[{j: meta_kmeans.labels_[n_clusters*i+j] for j in range(n_clusters)} for i in range(n_estimators)]
Para fazer o agrupamento dos clusters individuais, fazemos algum tipo de agrupamento (como a média, pensando em uma votação simples) dos diferentes clusters para obter um índice de pertencimento de cada exemplo a cada cluster.
from sklearn.preprocessing import LabelBinarizer
lb = LabelBinarizer().fit(list(range(n_clusters)))
aggregated_predicts = \
np.array([lb.transform(np.array(list(map(map_dic.get, km.predict(X)))))
for km, map_dic in zip(km_list, meta_clusters_map)]).mean(axis=0)
aggregated_predicts.shape
(1617, 9)
Para analisar se o que encontramos parece fazer sentido, vamos tentar interpretar os metacentróides encontrados (ou seja, os centróides que encontramos quando rodamos o
sklearn.cluster.KMeans nos centróides dos sklearn.cluster.KMeans base). Como estamos mexendo com essa base de dígitos, podemos olhar para a imagem representada pelo plot do metacentróide de cada cluster final.fig, ax = plt.subplots(ncols=3, nrows=3, figsize=(4, 4))
plt.gray()
for i, j in product(range(3), range(3)):
ax[i, j].matshow(meta_kmeans.cluster_centers_[3*i+j].reshape(8, 8))
ax[i, j].set_xticks([])
ax[i, j].set_yticks([])
ax[i, j].set_title(f"Cluster {3*i+j} centroid", fontsize=8)
plt.tight_layout()

A inspeção visual nos permite dar nomes para os clusters seguindo o formato dos números, construindo o seguinte dicionário:
dict_cluster = {0: 2, 1: 4, 2: 8, 3: 6, 4: 0, 5: 5, 6: 3, 7: 1, 8: 7}
Para ver os clusters finais e em que regiões do espaço estão os nosso pontos associados a clusters incertos, vamos aplicar um
sklearn.manifold.MDS e, em seguida, um sklearn.manifold.TSNE para reduzir a dimensionalidade dos nossos dados.from sklearn.manifold import MDS, TSNE
X_emb = \
(TSNE(random_state=42).fit_transform(MDS(random_state=42).fit_transform(X)))
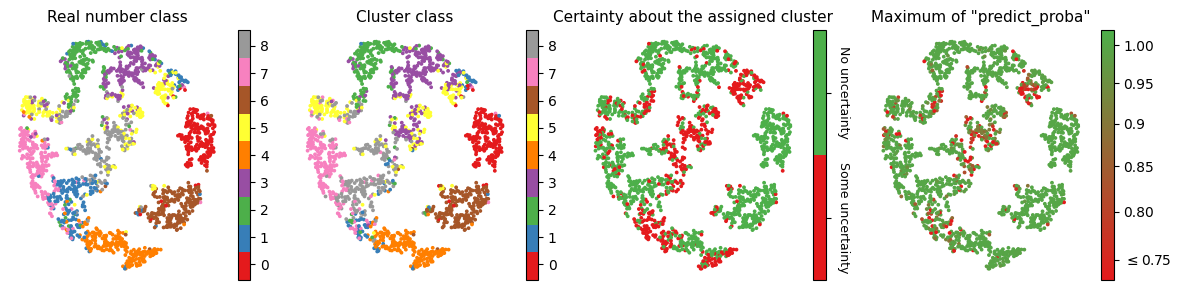
É legal ver que nossos clusters estão fazendo sentido com a marcação original de dígitos, mas o gráfico mais importante aqui é o último: vemos que de fato, existem exemplos que parecem ser mais confusos de atribuir a algum cluster de forma certa (como as imagens associadas ao número 8 que são facilmente confundidas com outros números e exemplos que parecem estar "na fronteira"; entre dois agrupamentos).
fig, ax = plt.subplots(ncols=4, figsize=(12, 3))
im0 = ax[0].scatter(X_emb[:, 0], X_emb[:, 1], s=3, c=digits.target , cmap="Set1")
cbar0 = plt.colorbar(im0, ax=ax[0], ticks=np.linspace(0.5, 7.5, 9))
cbar0.ax.set_yticklabels(np.arange(0, 9))
ax[0].set_title("Real number class", fontsize=11)
im1 = ax[1].scatter(X_emb[:, 0], X_emb[:, 1], s=3,
c=list(map(dict_cluster.get, aggregated_predicts.argmax(axis=1))),
cmap="Set1")
cbar1 = plt.colorbar(im1, ax=ax[1], ticks=np.linspace(0.5, 7.5, 9))
cbar1.ax.set_yticklabels(np.arange(0, 9))
ax[1].set_title("Cluster class", fontsize=11)
cmap2 = colors.ListedColormap(["#e41a1c", "#4daf4a"])
im2 = ax[2].scatter(X_emb[:, 0], X_emb[:, 1], s=3,
c=(aggregated_predicts.max(axis=1)==1).astype(int), cmap=cmap2)
im2.set_clim(0, 1)
cbar2 = plt.colorbar(im2, ax=ax[2], ticks=[0.25, 0.75])
cbar2.ax.set_yticklabels(["Some uncertainty", "No uncertainty"],
rotation=270, ha="center", rotation_mode="anchor", fontsize=9)
cbar2.ax.tick_params(pad=10)
ax[2].set_title("Certainty about the assigned cluster", fontsize=11)
cmap3 = colors.LinearSegmentedColormap.from_list('', colors=["#e41a1c", "#4daf4a"])
im3 = ax[3].scatter(X_emb[:, 0], X_emb[:, 1], s=3,
c=aggregated_predicts.max(axis=1), cmap=cmap3, norm=colors.LogNorm())
im3.set_clim(0.73, 1.02)
cbar3 = plt.colorbar(im3, ax=ax[3], ticks=[0.75, 0.8, 0.85, 0.9, 0.95, 1])
cbar3.ax.set_yticklabels(['$\leq$0.75', '0.80', '0.85', '0.9', '0.95', '1.00'])
ax[3].set_title('Maximum of "predict_proba"', fontsize=11)
for axs in ax:
clean_axes(axs)
plt.tight_layout()
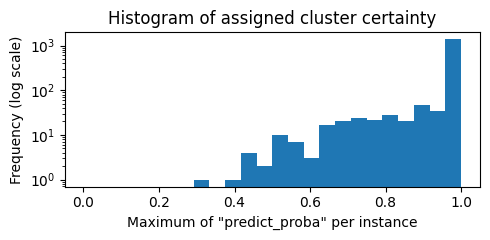
Observando o histograma do máximo do nosso "
.predict_proba", vemos que para um número razoável de exemplos, os clusters encontrados pelos agrupamentos individuais podem discordar ligeiramente gerando uma visão de incerteza e robustez associada à sua atribuição de agrupamento (ideia central dos algoritmos de soft clustering). Entretanto, para maioria dos exemplos os sklearn.cluster.KMeans individuais concordam totalmente.fig, ax = plt.subplots(figsize=(5, 2.5))
ax.hist(aggregated_predicts.max(axis=1), bins=np.linspace(0, 1, 25))
ax.set_yscale("log")
ax.set_xlabel('Maximum of "predict_proba" per instance')
ax.set_ylabel("Frequency (log scale)")
ax.set_title("Histogram of assigned cluster certainty")
plt.tight_layout()
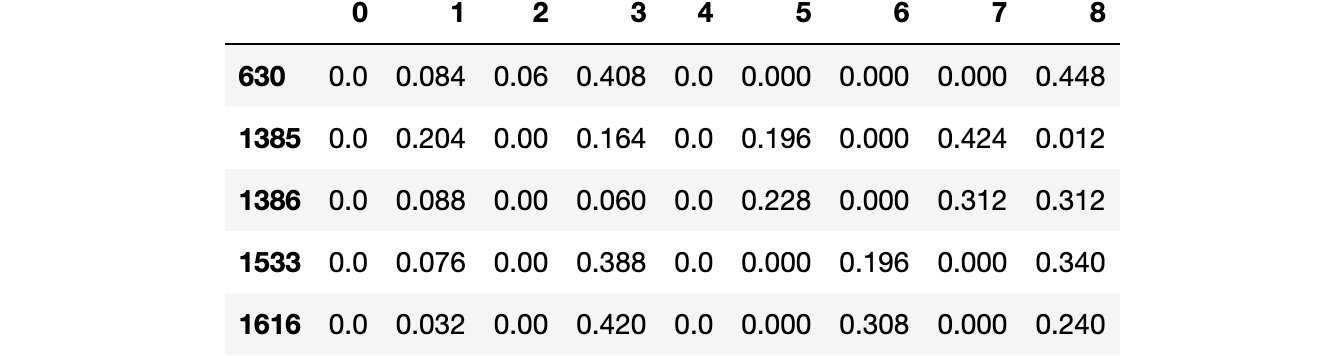
Essa visão nos permite ver os exemplos mais difíceis de agrupar, dando uma noção de instance hardness para o nosso problema de clusterização que, no nosso, exemplo parece estar associado a números parecidos com o 8.
(pd.DataFrame(aggregated_predicts)[(aggregated_predicts<0.45).all(axis=1)]
.rename(columns=dict_cluster).T.sort_index().T)
fig, ax = plt.subplots(ncols=5, figsize=(5, 2.5))
plt.gray()
for axs, i in zip(ax, pd.DataFrame(aggregated_predicts)[(aggregated_predicts<0.45).all(axis=1)].index):
axs.matshow(X[i].reshape(8,8))
axs.set_xticks([])
axs.set_yticks([])
axs.set_title(f"{i} - Target: {digits.target[i]}", fontsize=7)
plt.tight_layout()

Considerações finais
Essa ideia de clusterização de centróides não é nova e, inclusive, pode ser utilizada para definir a inicialização do K-Means. Esse algoritmo é chamado Refined K-Means [1], entretanto não parece ter uma vantagem clara quando comparado ao K-Means++ com múltiplas inicializações (maneira como o
sklearn.cluster.KMeans segue).Apesar de claramente ter aplicações em que vale a pena testar essa visão, nos experimentos feitos para construir essa discussão, os clusters encontrados individualmente raramente discordam muito (conseguimos ver isso pelo número significativo de exemplos com
aggregated_predicts.max(axis=1) sendo igual a 1) e os hard clusters encontrados no final da nossa estratégia de soft clustering (pegando o .argmax) são muito parecidos com os clusters encontrados em um K-Means usual. Portanto, não acho que seja uma técnica extremamente promissora, apesar de valer o teste sempre que você estiver interessado em um K-Means pelo baixo esforço adicional.unique_km_labels = KMeans(random_state=42).fit(X).labels_
(rand_score(unique_km_labels, aggregated_predicts.argmax(axis=1)),
(aggregated_predicts.max(axis=1)==1).mean())
(0.9799745280650514, 0.6951144094001237)
Por fim, é fácil generalizar as ideias aqui para qualquer outro algoritmo de clusterização baseado em centróides como o K-Medians ou o K-Medoids. Isso significa que não estamos necessariamente presos à distância euclidiana, que é a distância utilizada pelo K-Means.
Implementação grosseira da classe do estimador
Se você estiver interessado em utilizar essas ideias, elas deveriam funcionar utilizando algo na linha da classe implementada a seguir, que é compatível com bibliotecas que seguem o padrão de código do scikit-learn. Apenas fique atento ao caso em que
n_clusters=2, pois o sklearn.preprocessing.LabelBinarizer mantém apenas uma coluna ao invés de criar duas e, nesse caso, o return do seu .predict_proba terá apenas uma dimensão.import numpy as np
from sklearn.base import BaseEstimator
from sklearn.cluster import KMeans
from sklearn.preprocessing import LabelBinarizer
class MetaKMeans(BaseEstimator):
"""Meta K-Means clustering.
A Meta K-Means is a meta estimator that fits several K-Means
on various sub-samples of the dataset and uses averaging to
measure uncertainty related to predicted clusters.
Parameters
----------
n_clusters : int, default=8
The number of clusters to form as well as the number of
metacentroids to generate.
n_estimators : int, default=100
The number of K-Means in the ensemble.
random_state : int, default=42
Controls both the randomness of the bootstrapping of the samples used
when building the individual K-Means and the randomness of the
choice of initial centroids of each K-Means.
KMeans_params : dict, default={}
Explicitly set some of the base K-Means parameters as **KMeans_params.
"""
def __init__(self, n_clusters=8, n_estimators=100, random_state=42, KMeans_params={}):
self.n_clusters = n_clusters
self.n_estimators = n_estimators
self.random_state = random_state
self.KMeans_params = KMeans_params
def fit(self, X, y=None):
self.estimators_ = \
[KMeans(n_clusters=self.n_clusters, random_state=i+self.random_state, **self.KMeans_params)
.fit(X[np.random.RandomState(i).choice(X.shape[0], X.shape[0])])
for i in range(self.n_estimators)]
cluster_centers = np.vstack([km.cluster_centers_ for km in self.estimators_])
self.meta_kmeans_ = KMeans(n_clusters=self.n_clusters, random_state=42).fit(cluster_centers)
self.metacluster_centers_ = self.meta_kmeans_.cluster_centers_
self.meta_clusters_map_ = \
[{j: self.meta_kmeans_.labels_[self.n_clusters*i+j] for j in range(self.n_clusters)} for i in range(self.n_estimators)]
self.lb_ = LabelBinarizer().fit(list(range(self.n_clusters)))
return self
def predict_proba(self, X):
return \
np.array([self.lb_.transform(np.array(list(map(map_dic.get, km.predict(X)))))
for km, map_dic in zip(self.estimators_, self.meta_clusters_map_)]).mean(axis=0)
def predict(self, X):
return self.predict_proba(X).argmax(axis=1)
class_meta_kmeans_with_params = \
MetaKMeans(n_clusters=9, n_estimators=10, random_state=0, KMeans_params={"init": "random"}).fit(X)
class_meta_kmeans = \
MetaKMeans(n_clusters=9, n_estimators=250, random_state=0).fit(X)
class_predict_probas = class_meta_kmeans.predict_proba(X)
# As I'm choosing the same random_state, I expect results of the class
# to match the ones we did above.
((class_predict_probas == aggregated_predicts).all(),
(class_meta_kmeans.predict(X) == aggregated_predicts.argmax(axis=1)).all())
(True, True)
Referências
Todos os arquivos e ambiente para reprodução dos experimentos podem ser encontrado no repositório deste post.