Em construção: pequenos ajustes de formatação do LaTeX e exemplos de código
Vamos discutir a motivação da avaliação de modelos e dar ideias de como fazê-la. Em seguida, daremos um exemplo de como a variabilidade da amostra pode atrapalhar no cálculo das estatísticas de erro quando queremos otimizar hiper-parâmetros. E, por fim, vamos apresentar a validação com o método k-Fold como alternativa, minimizando a variância.
Avaliando a generalização de um modelo
Investigar qual é o desempenho real do nosso modelo em dados nunca vistos é uma tarefa importante e difícil, que deve ser feita minimizando os efeitos particulares da amostra que temos. Se queremos criar um modelo para fazer previsões, não adianta que a função hipótese tenha ótimos resultados nos dados que são utilizados no treinamento, se, quando dados novos surgirem, o modelo falhar em sugerir a variável alvo.
Vamos estudar esse efeito com um exemplo de regressão. Suponha que tenhamos o vetor aleatório $(X,Y)$ de forma que $X\sim\textrm{Uniforme}([-2,2])$ e
\[\begin{equation*} Y\sim 0.6X^3-2X^2-X+2+\varepsilon, \end{equation*}\]em que o ruído $\varepsilon$ é uma variável aleatória tal que $\varepsilon\sim \mathcal{N}(0,0.1)$.
def f(X):
return np.power(x, 3)*0.6 - np.power(x, 2) - x + 2
def f_ruido(X):
'''
input
- X: amostra da variável explicativa X (numpy array)
output
- amostra associada a Y com o ruído (float)
'''
return f(X) + np.random.normal(0, 0.1, size = X.shape[0])
def sample(n):
'''
input
- n: tamanho da amostra (inteiro)
output
- retorna uma amostra da distribuição conjunta (X,Y) (numpy array, numpy array)
'''
X = np.random.uniform(-2, 2, size=n)
Y = f_ruido(X)
return X.reshape(-1, 1), Y.reshape(-1, 1)
Peguemos uma pequena amostra com apenas $20$ exemplos que pode ser vista na Figura 1.
X, Y = sample(20)
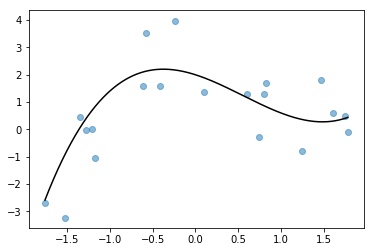
Vamos aproximar nossos dados com uma regressão polinomial. Explicando este algoritmo brevemente: dado $n\in\mathbb{N}$, induzimos “novas” variáveis através de $X$ da forma $X_i=X^i$ para $i\in\{ 0, 1, \cdots, n \}$. Aplicamos então uma regressão linear múltipla nas variáveis $X_i$ criadas (neste caso, sem o intercepto pois ele está representado por $X_0=1$), encontrando os coeficientes $a_i$ que minimizam a soma dos resíduos ao quadrado, ficando com o modelo
\[\begin{equation*} f(x) = a_0 + \sum_{i=1}^n a_i x^i. \end{equation*}\]Há um hiper-parâmetro que precisamos determinar antes do treinamento: o grau $n$ do polinômio. Isso gera toda uma família de funções hipóteses possíveis, indexada pelo valor de $n$. Mas qual destas funções devemos escolher? Ingenuamente, poderíamos acreditar que um modelo com erro baixo no treino nos geraria um modelo com erro baixo quando testado em dados futuros. Vamos ver que este nem sempre é o caso.
Nos dados anteriores, podemos fazer o polinômio de grau $19$ usando o método discutido anteriormente. A menos de erros de arredondamento na resolução do sistema linear (e possivelmente azar caso tenhamos dois valores de $X$ idênticos) o polinômio encontrado pelo algoritmo é exatamente o polinômio interpolador de Lagrange. Neste caso, o MSE é rigorosamente 0, pois o nosso polinômio passará por todos os dados. Temos seu gráfico na Figura 2.
pf = PolynomialFeatures(degree = 9, include_bias= True)
lr = LinearRegression(fit_intercept=False)
lr.fit(pf.fit_transform(X),Y)
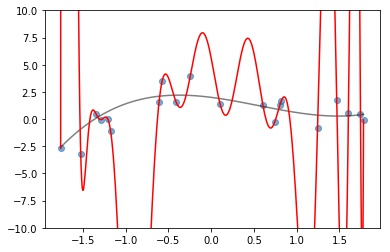
Este polinômio tem (praticamente) erro zero, mas graficamente vemos que ele não aprendeu o padrão dos dados, ele apenas decorou as observações que a gente tinha nos dados de treino. Para ver isso numericamente, podemos criar uma nova amostra da mesma distribuição que gerou os dados de treino, prever seus valores de $Y$ utilizando o polinômio e calcular o valor de $R^2$.
X_new, Y_new = sample(100)
print('R^2 no treinamento: ',r2_score(Y, lr.predict(pf.fit_transform(X))))
print('R^2 em um novo conjunto: ', r2_score(Y_new, lr.predict(pf.fit_transform(X_new))))
R^2 no treinamento: 1.0
R^2 em um novo conjunto: -12.241709591979532
Como o MSE no treinamento é virtualmente 0, o $R^2$ do treino é 1, nos dando a falsa impressão que temos um modelo perfeito e que encontramos exatamente a função que descreve os dados. Mas nos exemplos novos gerados pela mesma função, ficamos com um $R^2$ baixíssimo de $-12.242$.
Claramente, temos overfit. O modelo não aprendeu o padrão de criação dos dados, apenas decorou o que acontece nos dados de treino. Isso compromete a sua sua generalização para observações desconhecidas.
Seleção de modelos com hold-out
A maneira que começamos a resolver esse problema é parecida com a forma como identificamos ele. Agora, ao invés de usar todos os nossos dados iniciais para treinamento, vamos separa-los em duas partes: uma parte para treino e uma parte para validação. Essa maneira é conhecida como validação hold-out.
Agora, usamos dados de treinamento para treinar nossos vários modelos e em seguida, nos dados de teste, calculamos alguma métrica de erro. Como o processo de geração dos dados de treino e teste é o mesmo, estamos avaliando o modelo em dados que tem o mesmo padrão dos exemplos de treinamento, mas não são os mesmos. Assim, conseguimos avaliar os modelos pelas métricas, mas descartando modelos que apenas decoraram as respostas.
A ideia do hold-out na avaliação de um modelo $\widehat{f}_\alpha$, em que $\alpha\in \Omega$ é uma escolha de hiper-parâmetro entre todas as possíveis do conjunto $\Omega$ (no nosso caso, $\alpha$ é o grau do polinômio e $\Omega \subset \mathbb{N}$) pode ser resumida como:
- Dividimos nossos dados em um conjunto de treino e um conjunto de teste.
- Para cada $\alpha\in\Omega$, treinamos o modelo com o conjunto de dados de treino. Em seguida avaliamos o modelo com o conjunto de dados de teste. O valor obtido é então a nossa estimativa para erro do modelo \(\begin{equation*}\widehat{f}\_\alpha\end{equation*}\) em dados não vistos. Chamamos esta quantidade de $\widehat{E}_\alpha$.
- Com as estimativas para o erro, avaliamos os pontos $\{(\alpha, \widehat{E}_\alpha): \alpha \in \Omega\}$ e escolhemos o valor de $\alpha$ que mais nos agrade. Em muitos contextos é comum escolher $\alpha^* = \arg\min_{\alpha \in \Omega} \widehat{E}_\alpha$.
Essa abordagem de validação já resolve vários dos nossos problemas. Mas ainda há um fator que pode nos atrapalhar. Ficamos dependentes de como separamos nossa amostras de treino e de teste. Uma quebra infeliz pode gerar um viés indesejado nas estatísticas calculadas.
Se a distribuição dos dados de teste for muito diferente da distribuição dos dados de treinamento, podemos beneficiar ou atrapalhar o desempenho de alguns dos modelos. Nos dados anteriores, imagine que tivéssemos o modelo $A$ que é muito bom para $X$ negativos, e muito ruim para $X$ positivos. E um modelo $B$ que funciona melhor que $A$ no geral, pois acerta bastante para $X$ qualquer, mas não é tão bom quanto $A$ para valores negativos. Neste caso, se nosso conjunto de teste privilegiasse valores negativos de $X$, poderíamos escolher o modelo $A$ sobre o modelo $B$, mesmo isso sendo pior na média. Quando a distribuição de teste e treino são diferentes, temos um problema de train/test missmatch.
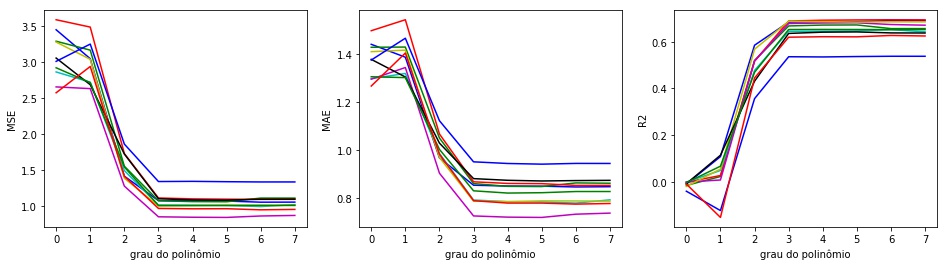
Para ilustrar essa variabilidade de acordo com a quebra que fazemos, vamos simular vários train_test_split diferentes nos nossos dados, fazendo o procedimento discutido anteriormente para escolher o grau do polinômio da regressão por mínimos quadrados.
Estamos apenas alterando a forma como quebramos entre treino e teste (variando a random_state do train_test_split). O conjunto de dados não muda. Ainda assim, isso é suficiente para termos curvas diferentes para cada quebra como vemos na Figura 3.
def varios_cortes_train_test(X, Y, quantidade_cortes = 5, grau_maximo = 7):
"""
nilvo
"""
dic = {'quebra': [], 'grau': [], 'MAE': [], 'MSE': [], 'R2': []}
for quebra in range(1, quantidade_cortes + 1):
for grau in range(0, grau_maximo + 1):
pf = PolynomialFeatures(degree =g rau)
X_ = pf.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_, Y, shuffle = True, test_size = 0.2, random_state = quebra)
lr = LinearRegression()
lr.fit(X_train, y_train)
dic['quebra'].append(quebra)
dic['grau'].append(grau)
dic['MAE'].append(mean_absolute_error(y_test,lr.predict(X_test)))
dic['MSE'].append(mean_squared_error(y_test,lr.predict(X_test)))
dic['R2'].append(r2_score(y_test,lr.predict(X_test)))
df = pd.DataFrame(dic)
plot_metricas_por_grau(df, quantidade_cortes)
def plot_metricas_por_grau(df, quantidade_cortes, metrica_list = ['MSE','MAE','R2']):
"""
wtf
"""
plt.figure(figsize=(16, 4))
for j, metrica in zip(range(1, len(metrica_list) + 1), metrica_list):
plt.subplot(1, len(metrica_list), j)
for i, c in zip(range(1, quantidade_cortes + 1), cycle('bgrcmyk')):
plt.plot(df['grau'][df['quebra'] == i], df[metrica][df['quebra'] == i], color = c)
plt.ylabel(metrica)
plt.xlabel('grau do polinômio')
plt.savefig('imagem3.jpg', bbox_inches = 'tight')
plt.show()
Seleção de modelos com k-Fold
A ideia aqui é usar todos os dados possíveis no treino e no teste, minimizando a variância associada com a quebra entre treino e teste. Vamos discutir a ideia do algoritmo k-Fold na otimização de hiper-parâmetros como fizemos na apresentação do hold-out.
Dividimos nossos dados em $ k$ conjuntos de (aproximadamente) mesmo tamanho, também chamados de pastas $1, 2, 3, \cdots, k$.
Fixado $i\in\{1,2,\dots,k\}$ e $\alpha \in \Omega$, treinamos o modelo $\widehat{f}_\alpha^{\,i}$ nas pastas $1,2,\cdots,i-1,i+1,\cdots,k$ e medimos suas métricas de avaliação na pasta $i$, obtendo o erro $E_\alpha^{\,i}$. Este procedimento é feito para cada $i\in\{1,2,\dots,k\}$ e para cada $\alpha\in\Omega$.
Por fim, valor estimado para erro do modelo $\widehat{f}_\alpha$ para dados não vistos é dado por
\[\begin{equation*} \widehat{E}_\alpha = \sum_{i=1}^k E_\alpha^{\, i}. \end{equation*}\]Com essas estimativas para o erro, avaliamos os pontos $\{(\alpha, \widehat{E}_\alpha): \alpha \in \Omega\}$ e escolhemos o valor de $\alpha$ que mais nos agrade. Em muitos contextos podemos escolher $\alpha^* = \arg\min_{\alpha \in \Omega} \widehat{E}_\alpha$.
No nosso exemplo, fazer a validação com o k-Fold, com $ k=5$, nos dá estimativas muito menos variáveis quando mudamos o random_state como podemos ver na Figura 4.
def varios_cortes_cross_validate(X, Y, quantidade_cortes = 10, grau_maximo = 7):
"""
nilvo
"""
dic = {'quebra': [], 'grau': [], 'MAE': [], 'MSE': [], 'R2': []}
for quebra in range(1, quantidade_cortes + 1):
kfold = KFold(n_splits = 5, shuffle = True, random_state = quebra)
for grau in range(0, grau_maximo + 1):
pf = PolynomialFeatures(degree = grau)
X_ = pf.fit_transform(X)
aux = pd.DataFrame(cross_validate(lr, X_, Y, scoring = ['r2', 'neg_mean_squared_error', 'neg_mean_absolute_error'], cv = kfold, return_train_score = False))
dic['quebra'].append(quebra)
dic['grau'].append(grau)
dic['MAE'].append(-aux.mean()['test_neg_mean_absolute_error'])
dic['MSE'].append(-aux.mean()['test_neg_mean_squared_error'])
dic['R2'].append(aux.mean()['test_r2'])
df = pd.DataFrame(dic)
plot_metricas_por_grau(df, quantidade_cortes)
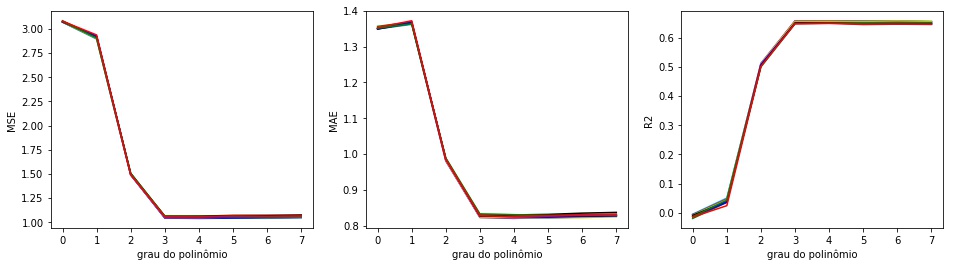
Neste caso, temos estimativas muito mais seguras para o valor do erro em cada valor do grau do polinômio e não precisamos de mais dados para isso. Precisamos apenas de uma maneira mais inteligente de validar nosso modelo.
Uma dúvida que pode surgir é: porque não fazer $k$ validações hold-out tradicionais? Porque fazer a quebra em pastas? A divisão em pastas nos garante que todos os dados estão sendo usados para teste, isso nos deixa mais seguros minimizando o efeito de train/test missmatch.
Comentei que dependo do problema podemos escolher $\alpha^*\in\Omega$ de maneira diferente. Por exemplo, no nosso caso, é possível optar pelo grau do polinômio ideal como sendo $2$ ou $3$, valores em que temos os maiores ganhos de redução da métrica. A ideia neste caso seria que simplicidade também é importante, então mesmo que o grau do polinômio que teria o menor erro seja alto, priorizamos modelos menos complicados.
Observação complementar a respeito de aproximações polinomiais
O Teorema de Stone-Weierstrass nos garante que, para qualquer função real contínua $g:I\to\mathbb{R}$ tal que o domínio $I$ é um intervalo fechado (mais geralmente, um compacto), existe uma sequência de polinômios que converge uniformemente para $g$. Isso nos garante que, dada uma tolerância $\delta>0$, existe um polinômio $p$ de grau suficientemente grande tal que $|g(x)-p(x)|<\delta$ para todo $x\in I$.
Portanto, a abordagem de aproximação polinomial pareceria muito promissora. Entretanto o Teorema de Stone-Weierstrass nos garante a existência do polinômio, mas não nos da uma maneira construtiva de encontra-lo. Além disso, o problema aqui é diferente: não sabemos a forma de $f$, temos apenas o valor aproximado dela em alguns pontos. Estimar sua forma a partir de interpolação polinomial nos gera polinômios que não se comportam bem fora de pontos amostrados quando aumentamos o número de dados (e consequentemente o grau do polinômio interpolador). Além disso, o cálculo numérico carrega erros de arredondamento que geram resultados estranhos. Uma alternativa um pouco melhor é utilizando splines.