Texto em construção: Pequenas alterações de formatação.

Este post faz parte de uma série de postagens que discutem o problema de covariate shift. Assumo que você já conhece a motivação do problema e no que estamos interessados em identificar e corrigir. Se você ainda não leu o primeiro post dessa série, sugiro a leitura.

Agora, vamos forcar em identificar o covariate shift na distribuição conjunta. Desta forma, o problema fica enunciado como: dados $X$ e $Z$ vetores aleatórias e dois conjuntos de observações amostrados de forma independente $\{x_1, x_2, \cdots, x_N \} $ e $\{z_1, z_2, \cdots, z_M \} $, queremos entender se a distribuição conjunta é a mesma, isto é se $X\sim Z$, estudando apenas as amostras coletadas. No contexto do dataset shift, que estamos particularmente interessados, o vetor aleatório $X$ indica a distribuição das covariáveis no conjunto de treino e o vetor aleatório $Z$ nos revela a distribuição das variáveis explicativas dos dados em produção.

Anteriormente, no segundo post da série, discutimos uma técnica para encontrar mudança nas distribuições marginais dos vetores aleatórios, o QQ-plot. Sugerimos ainda uma variação numérica da técnica visual.

Agora, vamos utilizar aprendizado de máquina supervisionado para identificar problemas em aprendizado de máquina supervisionado.

Entendendo o problema de classificação

O problema de classificação binária surge naturalmente nesse cenário. Se temos duas amostras de distribuições possivelmente diferentes, podemos treinar um modelo que tenta identificar se os dados são da distribuição $X$ ou da distribuição $Z$. Se as distribuições são

Se o classificador binário consegue identificar as diferenças, então temos uma variação da distribuição. Se o classificador não consegue, mantendo uma acurácia baixa, então confiamos que a distribuição se manteve parecida.

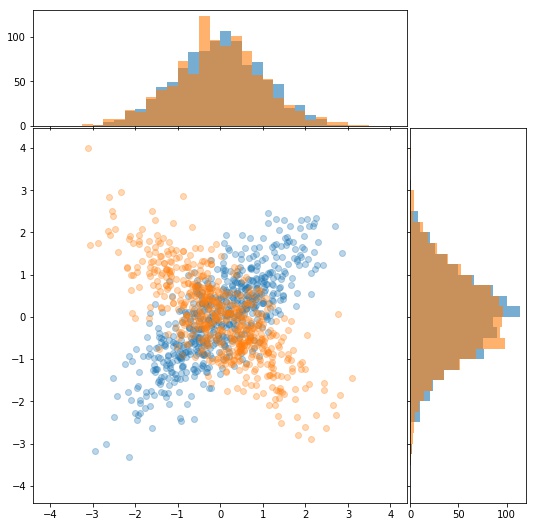
Vamos ilustrar essa técnica nos dados que geraram o desconforto inicial apresentado no final da [postagem anterior](to die by ur side). Aqui fica claro que nem sempre analisar apenas as distribuições marginais é suficiente.

Explicitamente temos os vetores aleatório $X= (X_1,X_2)$ e $Z=(Z_1, Z_2)$ tal que

\[\begin{equation*} \begin{pmatrix}X_{1}\\ X_{2} \end{pmatrix} \sim \mathcal{N} \begin{pmatrix} \begin{bmatrix} 0\\ 0 \end{bmatrix} , \begin{bmatrix} 1 & 0.75 \\ 0.75 & 1 \end{bmatrix} \end{pmatrix} \textrm{, e }\begin{pmatrix}Z_{1}\\ Z_{2} \end{pmatrix} \sim \mathcal{N} \begin{pmatrix} \begin{bmatrix} 0\\ 0 \end{bmatrix} , \begin{bmatrix} 1 & -0.75 \\ -0.75 & 1 \end{bmatrix} \end{pmatrix} . \end{equation*}\]

def sample(n, t = 1):
    return np.random.multivariate_normal(mean = [0,0], cov = [[1,t*0.75], [t*0.75,1]], size = n).T

X1, X2 = sample(1000)
Z1, Z2 = sample(1000, -1)

Figura 1: Dados .

A ideia é simples, vamos organizar nossos dados criando uma nova coluna que nos diz de o dado é da distribuição $X$ ($s=0$) ou da distribuição $Z$ ($s=1$).

df = pd.DataFrame({'variavel_1':np.concatenate([X1,Z1]), 'variavel_2':np.concatenate([X2,Z2]), 's':[0]*X1.shape[0]+[1]*Z1.shape[0]})

X_miss = np.asarray(df.drop(['s'],axis=1))
S_miss = np.asarray(df['s'])

variável 1	variável 2	y	s
0.178105	0.651739	$y_1$	0
0.464192	-0.461877	$y_2$	0
1.0948	0.823703	$y_3$	0
…	…	…	…
0.393783	-0.681826	?	1
0.623834	-0.344885	?	1
-0.800357	0.444416	?	1

Aqui, já fazendo um panorama com a realidade em que estamos aplicando esse modelo, coloquei uma coluna para a variável target $y$ que seria a variável alvo do nosso problema inicial. Não vamos usar ela em nenhum momento na identificação do covariate shift, o que é esperado já que não temos os targets dos dados novos encontrados na produção.

Com essa estrutura construída, a ideia é simples. Criamos um classificador que utiliza as variáveis 1 e 2 para prever $s$. Se o seu resultado em um conjunto de teste é ruim, então os dados de $X$ e $Z$ são indistinguíveis e concluímos que $X\sim Z$. Agora, se o nosso classificador tem boas métricas, então quer dizer que as distribuições diferem.

Construindo e avaliando o classificador binário

Primeiro, separamos nossos dados em 2 conjuntos. Um para treino e outro para teste.

X_miss_train, X_miss_test, S_miss_train, S_miss_test = train_test_split(X_miss, S_miss, test_size = 0.8)

Agora podemos utilizar o classificador binário qualquer. Como estou começando a me apaixonar pelo Vapnik, vou utilizar uma Support Vector Machine. Os hiper-parâmetros "default" das SVM costumam fazer um bom trabalho, mas em um mundo ideal, podemos fazer uma pequena otimização dos hiper-parâmetros maximizando a métrica roc_auc_score.

param = {'C': np.geomspace(0.01,100,13), 'gamma': ['scale']+list(np.geomspace(0.1,100,10)), 'kernel' = ['rbf']}
grid_search = GridSearchCV(SVC(probability=True), param, cv = 5, scoring= ['roc_auc','accuracy'], refit = 'roc_auc', return_train_score=True)
grid_search.fit(X_miss_train, S_miss_train)

Em seguida, utilizamos o modelo encontrado em todos os dados e podemos avaliar seu desempenho.

svm = SVC(probability=True, **grid_search.best_params_)
svm.fit(X_miss_train,S_miss_train)

print('acuracia: ',accuracy_score(S_miss_test,svm.predict(X_miss_test)))
print('roc_auc: ',roc_auc_score(S_miss_test,svm.predict(X_miss_test)))
print('phi coeficiente: ',matthews_corrcoef(S_miss_test,svm.predict(X_miss_test)))

acuracia:  0.72625
roc_auc:  0.7268930344332967
phi coeficiente:  0.4827618287310226

Não temos uma acurácia estado da arte, mas claramente nosso modelo identificou um padrão e consegue discriminar dados como sendo de uma distribuição ou de outra.

$\oint$  Uma métrica não tão clássica, mas muito útil é o coeficiente de correlação de Matthews. Inspirado no coeficiente de correlação de Pearson, queremos entender correlação para atributos categóricos. Isso deu origem ao coeficiente phi de Pearson, a ideia dele é generalizar o coeficiente de correlação entre a nossa previsão e os valores reais da target binária. É uma forma numérica de avaliar a matriz de confusão. Seu cálculo é feito como

\[\begin{equation*} \textrm{MCC} = \frac{T_p \, T_n - F_p \, F_n}{\sqrt{(T_p+F_p)(T_p+F_n)(T_n+F_p)(T_n+F_n)}}, \end{equation*}\]

em que $T_p$ é o número de verdadedeiros positivos, $T_n$, a quantidade de verdadeiros negativos, $F_p$ o número de falsos positivos e $F_n$ o número de falsos negativos. Apesar de parecer um pouco confuso, analisando o numerador vemos que estamos multiplicando os valores corretamente classificados e subtraindo a multiplicação dos incorretamente classificados. O denominador serve como uma normalização deixando o resultado entre $-1$ e $1$, em que $1$ significa uma previsão perfeita, $0$ uma previsão aleatória e $-1$ uma previsão trocada.

No nosso caso ilustrativo em duas dimensões, podemos fazer as curvas de nível do predict_proba do SVM e visualizar que ele entendeu as regiões mais prováveis de cada uma das distribuições.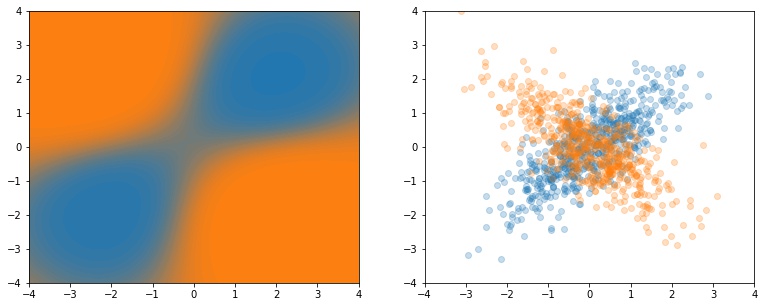

Figura 2: Dados .

$\oint$ O SVM não nos da naturalmente o predict_proba, precisamos passar probability=True na sua inicialização. O sklearn aplica a abordagem de Platt utilizando uma regressão logística no score do SVM. Essa técnica pode ser utilizada com classificadores quaisquer, para melhorar a calibração de probabilidade. Inclusive é uma técnica útil para ensembles de árvores.

Entendendo a mudança na distribuição a partir do classificador

Agora precisamos avaliar se as distribuições são diferentes ou não. Podemos analisar um histograma dos predict_proba aplicado nas duas amostras separadamente como vemos na Figura 3. Claramente, nosso SVM identifica regiões em que a chance de ser de uma das distribuições é maior do que ser de outra. Ele nos dar tanta certeza é um indicativo de que ele consegue distinguir bem.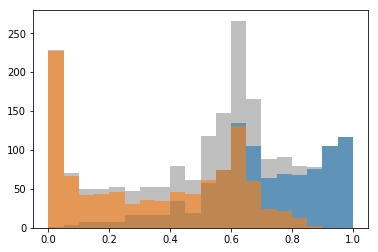

Figura 3: Dados .

Supondo que confiamos na medida de probabilidade que ele nos dá. Uma métrica um pouco arbitrária é olhar qual a porcentagem dos dados está na região entre $[0, x) \cup (0.5+x,1]$ para $0\leq x\lt 0.5$. Por exemplo, podemos olhar a proporção de exemplos com predict_proba de $0$ a $25\%$ ou de $75\%$ a $100\%$. Estes são os dados que o classificador julga como "fáceis de classificar" por estarem em regiões dominadas por alguma das classes.

x = 0.25
((svm.predict_proba(X_miss)[:,0]<0.5-x) | (svm.predict_proba(X_miss)[:,0]>0.5+x)).sum()/X_miss.shape[0]

0.4605

Quase metade dos dados estão nas regiões "fáceis" de acordo com essa análise de probabilidade. Claro que isso não é perfeito pela existência de outliers, mas é um indicativo claro de que existem regiões do espaço de atributos favorecidas por uma das distribuições e regiões do espaço favorecidas pela outra distribuição. Fixado $x$, podemos escolher um valor $\varepsilon\in(0,1]$ tal que: se a proporção de dados nas regiões "fáceis" for maior que $\varepsilon$ então temos um alerta que há uma mudança na distribuição.

Podemos tentar criar também thresholds de acurácia ou do coeficiente phi que indicam que há uma mudança na distribuição ou não. Isso não é necessariamente claro também e podemos gerar monitorar com rigor demais ou sendo muito brandos.

Como discutido no post anterior, esses tresholds universais não existem. O que vale é analisar nos seus dados históricos casos de covariate shift que você sabe que aconteceram e analisar se existiria um $\varepsilon$ que teria funcionado neles.

Caso sem mudança

Vale estudar como essa metodologia se comportaria em casos em que não há mudança na distribuição. Por exemplo, se ambas as distribuições fossem geradas pela mesma normal multivariada dada por

\[\begin{equation*} \begin{pmatrix}X_{1}\\ X_{2} \end{pmatrix}, \begin{pmatrix}Z_{1}\\ Z_{2} \end{pmatrix} \sim \mathcal{N} \begin{pmatrix} \begin{bmatrix} 0\\ 0 \end{bmatrix} , \begin{bmatrix} 1 & 0.75 \\ 0.75 & 1 \end{bmatrix} \end{pmatrix}. \end{equation*}\]

X1, X2 = sample(1000)
Z1, Z2 = sample(1000)

Fazendo exatamente os mesmos procedimentos que anteriormente, temos agora curvas de nível muito mais confusas como vemos na Figura 4. O classificador tenta se adaptar um pouco às particularidades das amostras, mas não se atreve a dar probabilidades altas para nenhuma das regiões justamente porque nenhuma das regiões é privilegiada por uma das distribuições neste caso.

Figura 4: Dados .

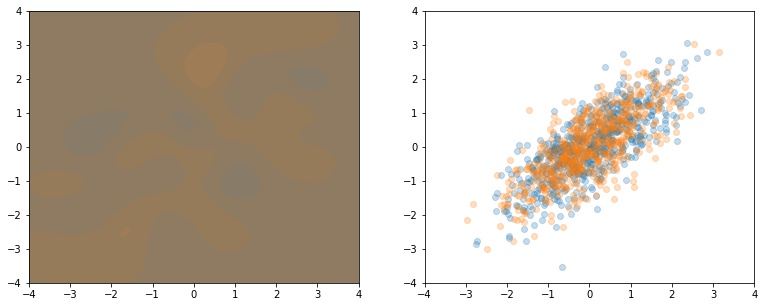
Isso fica ainda mais claro quando olhamos para as métricas de classificação neste caso. Fica claro que as distribuições são indistinguíveis nesse caso, como esperado.

acuracia:  0.511875
roc_auc:  0.5115329746824565
phi coeficiente:  0.023459774068708163

A análise da distribuição dos predict_proba também conversa com o que esperávamos. Agora, o modelo é muito mais conservador, colocando as probabilidades próximas de $0.5$ como vemos na Figura 5.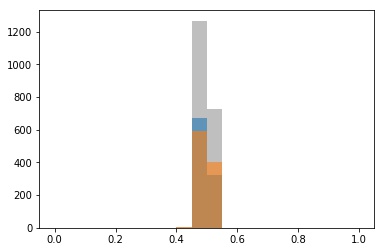

Figura 5: Dados .

Neste caso, os predict_proba estão concentrados entre $0.4$ e $0.6$, como esperado. O modelo é conservador e não encontra regiões fáceis de classificação.

x = 0.1
((svm.predict_proba(X_miss)[:,0]<0.5-x) | (svm.predict_proba(X_miss)[:,0]>0.5+x)).sum()/X_miss.shape[0]

0.0

Pontos de atenção e considerações finais

Assim como a maioria das técnicas de monitoramento, não é necessariamente claro identificar se há ou não o covariate shift categoricamente. A criação de thresholds para alertas é nebulosa. A ideia é sempre utilizar várias formas de avaliar, gerando relatórios que precisam ser olhados de forma crítica.

Em muitos casos, toda essa análise com otimização de hiper-parâmetros e utilizando modelos custosos como o SVM pode ser inviável. Não precisamos ter um classificador binário estado da arte, ele só precisa ser bom o suficiente para conseguir aprender a identificar as regiões de cada uma das amostras (se existir) dando probabilidades adequadas. Logo, fique a vontade para escolher o classificador que você mais gostar, com o cuidado na hora das análises do predict_proba. Como comentei anteriormente, os parâmetros default das SVM costumam ser razoáveis e você pode sempre pegar algumas sub-amostras dos dados para fazer essas análises.

É razoável se preocupar também com o balanceamento entre o tamanho dos dados de treino ($s=0$) e dados de produção ($s=1$) para ser razoável analisar acurácia e métricas simples. Novamente, lembrando que esse classificador não precisa ser perfeito, um undersample da classe dominante me parece suficiente.

Essa técnica incorporada em linhas de produção robustas pode ser uma forma inteligente de identificação de variação das covariáveis de treino e produção. No próximo post utilizaremos o princípio da minimização do erro empírico de Vapnik para discutir porque o covariate shift se torna um problema. Essa narrativa nos indicará uma maneira elegante de amenizar os problemas causados pelo covariate shift quando o retreino com dados mais parecidos com os da produção não é possível.