Covariate Shift: QQ-plot

Texto em construção: Pequenas alterações de formatação.

Este post faz parte de uma série de postagens que discutem o problema de Covariate Shift. Assumo que você já conhece a motivação do problema e no que estamos interessados em identificar e corrigir. Se você ainda não leu o primeiro post dessa série, sugiro a leitura.

Relembrando a reformulação do enunciado do problema, temos $X$ e $Z$ variáveis (ou vetores) aleatórias e dois conjuntos de observações amostrados de forma independente $\{x_1, x_2, \cdots, x_N \} $ e $\{z_1, z_2, \cdots, z_M \} $. Queremos entender se a distribuição das variáveis é a mesma, isto é se $X\sim Z$, estudando apenas as amostras coletadas. No contexto do dataset shift, que estamos particularmente interessados, o vetor aleatório $X$ indica a distribuição das covariáveis no conjunto de treino e o vetor aleatório $Z$ nos revela a distribuição das variáveis explicativas dos dados em produção.

A primeira técnica que vamos discutir é utilizando o QQ-plot (quantil-quantil-plot). Avaliando se os $\alpha$-quantis das duas amostras são parecidos, podemos discutir a validade de assumir $X\sim Z$ ou não.

$\alpha$-quantis de uma variável aleatória

Existem algumas formas diferentes de se calcular $\alpha$-quantis. Elas são mais ou menos equivalentes para as análises que estamos interessados, então não vamos detalhar pequenas variações. Começaremos discutindo um $\alpha$-quantil muito clássico que você já conhece: a mediana.

A mediana de um conjunto de dados é o valor real que divide nossos dados em dois subconjuntos de tamanhos iguais: os conjuntos maiores que a mediana e o conjunto menores ou iguais à mediana. Por exemplo, se temos o conjunto $S =\{ 1, 2, 4, 6, 6, 9\}$, então a mediana pode ser $4$ já que ficamos com $|\{x \in S : x\leq 4 \}|$ $ = 3 =$ $ |\{x \in S : x\gt 4 \}|$.

O conceito de mediana pode ser estendido para variáveis aleatórias. Nesse caso, estamos interessados em procurar um valor real $p$ tal que a probabilidade da variável aleatória ser menor ou igual a $p$ seja 0.5. Isso significa que o valor $p$ divide a reta em duas regiões $\{ x\in\mathbb{R}:x\leq p \}$ e $\{ x\in\mathbb{R}:x\gt p \}$ com a mesma probabilidade, ou seja, $\mathbb{P(X\leq p)}$ $=0.5=$ $\mathbb{P}(X\gt p)$.

Dado $\alpha\in(0,1)$, a ideia de um $\alpha$-quantil de uma variável aleatória $X$ é uma generalização do que fizemos com a mediana. Queremos dividir a reta em duas regiões, uma com probabilidade $\alpha$ e a segunda com uma probabilidade $1-\alpha$. Na mediana, tínhamos $\alpha=0.5$, aqui é feito de forma análoga, mas mais geral. A ideia é que tenhamos que $q_X(\alpha)$, o $\alpha$-quantil de $X$, satisfaça a equação

\[\mathbb{P}\left( X\leq q_X(\alpha) \right) = \alpha.\]

Lembrando que $F_X(t) = \mathbb{P}(X\leq t)$ é a função de distribuição acumulada de uma variável aleatória $X$. A $q_X:(0,1)\to\mathbb{R}$, chamada função quantil, seria a inversa de $F_X$. Ou seja, $F_X(q_X(\alpha))=\alpha$. A mediana de uma variável aleatória $X$ é formalmente definida como $q_X(0.5)$.

Entretanto, podemos exibir variáveis aleatórias problemáticas tal que a equação não tem solução para alguns valores de $\alpha\in(0,1)$. Por exemplo, pegando $X\sim\textrm{Ber}(0.4)$, então não existe $p\in\mathbb{R}$ tal que $F_X(p ) = 0.5$ uma vez que

\[F_X(t) = \begin{cases} 0\textrm{, se }t\lt0, \\ 0.6\textrm{, se }0\leq t\lt 1,\\ 1\textrm{, se }t\geq1.\end{cases}\]

Dessa forma não conseguimos definir $q_X(0.5)$, a mediana da variável Bernoulli de parâmetro $0.6$ utilizando essa forma para função quantil.

Note também que no primeiro exemplo, para a mediana do conjunto $S$, a mediana não está unicamente determinada. Poderíamos ter pego a mediana como sendo $5$, já que este valor também dividiria nossos dados em conjuntos do mesmo tamanho.

Como queremos uma função bem definida, uma solução para esses problemas é fazer a função quantil tal que

\[\begin{equation*} q_X(\alpha) = \min \{t \in \mathbb{R} : \mathbb{P}(X\leq t) = F_X(t) \geq \alpha \}. \end{equation*}\]

Neste caso, o valor $q_X(\alpha)$ é o menor valor real tal que a probabilidade acumulada é pelo menos $\alpha$. No caso discutido para $X\sim\textrm{Ber}(0.4)$, agora temos que $q_X(0.5) = 0$ já que 0 é o menor valor real que faz $F_X$ ser maior ou igual a $0.2$. E a mediana do conjunto $S$ fica unicamente definida uma vez que $4$ é o menor valor que satisfaz a divisão em dois conjuntos iguais.

Para variáveis aleatórias $X$ tais que $F_X$ são contínuas, essa forma de definir $q_X(\alpha)$ equivale com a primeira tentativa de definição. Essas são os exemplos que estaremos mais interessados quando analisarmos o QQ-plot.

$\oint $ A generalização da inversa que fizemos é particularmente útil quando temos funções monotômicas, mas descontínuas e não necessariamente injetoras como é o caso das funções distribuições acumuladas de variáveis aleatórias discretas. A única alteração que temos que fazer em casos mais gerais é usar $\inf$ ao invés de $\min$ (pelas propriedades da função distribuição acumulada, como temos a continuidade pela direita, essas duas formas são equivalentes).

Cálculo da função quantil de uma variável aleatória contínua

Quando $X$ é uma variável aleatória contínua com distribuição de probabilidade $f_X$, temos uma forma explícita de cálculo para $F_X$ como

\[\begin{equation*} F_X(t) = \int_{-\infty}^t f_X(s) \, ds. \end{equation*}\]

Dada uma variável aleatória com distribuição exponencial $X\sim \textrm{Exp}(\lambda)$, vamos exibir diretamente $q_X$. Para calcular $F_X$, utilizamos a densidade de probabilidade $f_X$ da forma

\[\begin{equation*} f_X(s) = \begin{cases} \lambda e^{-\lambda s}\textrm{, se } s\geq 0\textrm{,}\\ 0 \textrm{, caso contrário.} \end{cases} \end{equation*}\]

Podemos calcular $F_X$ como

\[\begin{equation*} F_X(t) = \int_{-\infty}^{t} f_X(s) ds = \int_0^t \lambda e^{-\lambda s} ds = -\,e^{-\lambda s}\, \bigg\rvert_{0}^{t} = 1 - e^{-\lambda t}, \end{equation*}\]

para $t\geq 0$ e $F_X(t)=0$ para $t<0$.

Podemos achar uma forma explícita para $q_X(\alpha)$ neste caso. Basta resolver a equação:

\[\begin{equation*} \alpha = F_X(q_X(\alpha)) = 1 - e^{-\lambda q_X(\alpha)} \therefore 1- \alpha = e^{-\lambda q_X(\alpha)}, \end{equation*}\]

concluindo que

\[\begin{equation*} q_X(\alpha) = \frac{-\ln(1-\alpha)}{\lambda}. \end{equation*}\]
def dens_exp(s, lamb):
    return np.piecewise(s, [s < 0, s >= 0], [lambda s: 0, lambda s: np.exp(-lamb*s)/lamb])

def quantil_exp(t,lamb):
    return -np.log(1-t)/lamb

Por exemplo, se queremos calcular a mediana de $X\sim\textrm{Exp}(\lambda =1)$, fazemos simplesmente $q_X(0.5)=-\ln(0.5)\approx0.693$. Interpretando esse resultado, temos que $\mathbb{P}\left( X\leq -\ln(0.5) \right)=0.5$, logo pintando a área embaixo da curva, como na Figura 1, temos metade da área da densidade de probabilidade até $-\ln(0.5)$.

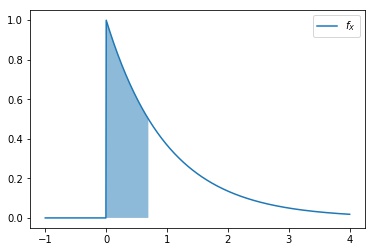
Figura 1: Densidade de probabilidade da variável aleatória exponencial com $\lambda=1$. A sombra representa a área embaixo da curva de 0 até $-\ln(0.5)$, representando metade da probabilidade.

Cálculo da função quantil de uma variável aleatória discreta

Agora suponha que $X\sim \textrm{Binomial}(2,0.5)$. Então $\mathbb{P}(X=0)=\mathbb{P}(X=2)= 0.25$ e $\mathbb{P}(X=1)=0.5$. Construímos a densidade acumulada como

\[F_X(t) = \begin{cases} 0\textrm{, se }t\lt0, \\ 0.25\textrm{, se }0\leq t \lt 1,\\ 0.75\textrm{, se }1\leq t \lt 2,\\ 1\textrm{, se }t\geq2.\end{cases}\]

Para calcular a função quantil, precisamos usar a versão que diz que

\[q_X(\alpha) = \min \{t \in \mathbb{R} : F_X(t) \geq \alpha \}.\]

Com isso, temos por exemplo que $q_X(0.9)=2$ uma vez que o menor valor de $F_X(t)$ maior ou igual a $0.9$ é $1$ e ocorre primeiro quando $t=2$. Fazendo esse mesmo tipo de raciocínio para todos os $\alpha \in (0,1)$, chegamos na função quantil como

\[q_X(\alpha) = \begin{cases} 0\textrm{, se }0\lt \alpha \leq 0.25, \\ 1\textrm{, se }0\lt \alpha \leq 0.75, \\ 2\textrm{, se }0.75\leq \alpha \lt 1.\end{cases}\]

QQ-plot

A ideia do QQ-plot (ou gráfico quantil-quantil) se baseia em uma observação inteligente: se duas variáveis aleatórias $X$ e $Y$ tem distribuições parecidas (isto é, se $F_X \approx F_Y$), então seus $\alpha$-quantis são semelhantes também (ou seja, as funções quantis são próximas $q_X \approx q_Y$).

Portanto, se $X$ e $Y$ têm distribuições parecidas, quando plotarmos a "curva parametrizada"

\[\begin{equation*} \{ (q_X(\alpha), q_Y(\alpha) ) \in \mathbb{R}^2 : \alpha \in (0,1) \}, \end{equation*}\]

esperamos que a curva fique próxima da reta identidade $y=x$ . O nome QQ-plot surge pois estamos plotando os quantis das nossas variáveis aleatórias nos dois eixos.

Para visualizar esse plot, vamos ver um exemplo analítico. Sejam $X \sim \textrm{Exp}(\lambda=1)$ e $Y \sim \textrm{Uniforme}([0,1])$. Já calculamos de forma transparente $q_X(\alpha)=-\ln(1-\alpha)$ e é fácil conferir que $q_Y(\alpha) = \alpha$.

def dens_uni(s):
    return np.piecewise(s, [s < 0, (s >= 0) & (s <= 1), s > 1], [0, 1, 0]) 
    
def quantil_uni(t):
    return t

Como podemos ver na primeira imagem da Figura 2, essas distribuições são próximas no ínicio (perto da origem) e depois ficam qualitativamente bem diferentes. Plotando a curva dada por

\[\begin{equation*} \{ (-\ln(1-\alpha), \alpha ) \in \mathbb{R}^2 : \alpha \in (0,1) \}, \end{equation*}\]

temos o QQ-plot na segunda imagem da Figura 2.

Figura 2: qqplot

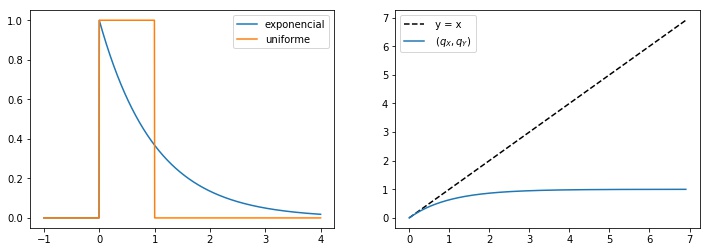
$\alpha$-quantis para amostras

Quando não conhecemos $F_X$, não temos como calcular $q_X(\alpha)$ analiticamente. Mas se temos disponível uma amostra $\left\{x_1,\ldots,x_N \right\}$ independentes e identicamente distribuídas de $X$ de tamanho $N$ podemos estimar os $\alpha$-quantis.

  • Primeiro, devemos ordenar a amostra $\left\{x_1,\ldots,x_N \right\}$ de forma crescente renomeando os índices dos exemplos como $\left\{ x_{(1)},\ldots,x_{(N)} \right\}$.

  • Com isso, dado $\alpha \in (0,1)$, a estimativa para o $\alpha$-quantil da variável aleatória que gerou a amostra é

    \(\begin{equation*} \widehat{q}_{X}(\alpha) = x_{( \lfloor N\alpha \rfloor +1)}, \end{equation*}\) em que $\lfloor N\alpha \rfloor$ é o menor inteiro menor ou igual a $N\alpha$.

A ideia dessa forma de estimar o $\alpha$-quantil é que uma fração $\alpha$ da nossa amostra será identificada como os elementos menores ou iguais a $\widehat{q}_X(\alpha)$. Na Figura 3 podemos observar alguns $\alpha$-quantis de uma amostra de dados para $N=40$. Plotando eles na horizontal, ordenados, identificamos o $0.25$-quantil como o décimo elemento da nossa lista, marcado em verde uma vez que $25$ por cento dos nossos dados são menores ou iguais a ele.

Figura 3: Uma coleção de dados colocado em ordem crescente e alguns $\alpha$-quantis ilustrativos.

Quando $N\to \infty$ temos que $\widehat{q}_{X}(\alpha) \to q_{X}(\alpha)$ em probabilidade, pelo menos para variáveis aleatórias contínuas. Isso nos permite acreditar que, para $N$ grande, o $\alpha$-quantil estimado é próximo do $\alpha$-quantil real, vamos usar esse fato para comparar nossas amostras.

QQ-plot para duas amostras

A idéia do QQ-plot é justamente utilizar essa ideia para afirmar que se a amostra $\left\{x_1,\ldots,x_N \right\}$ e a amostra $\left\{y_1,\ldots,y_M \right\}$ vieram de distribuições $X$ e $Y$, respectivamente, parecidas, então também serão parecidos as funções quantis estimadas

\[\begin{equation*} \widehat{q}_{X}(\alpha) \approx \widehat{q}_{Y}(\alpha). \end{equation*}\]

Neste caso, se parametrizamos uma curva pelo valor $\alpha$ e plotamos no eixo $x$ o valor $\widehat{q}_{X}$ e no eixo $y$ o valor $\widehat{q}_{Y}$, necessariamente devemos ter pontos próximos da reta identidade $y=x$.

Variando o parâmetro da curva com passos iguais, plotamos os pontos

\[\begin{equation*} \left\{ (\widehat{q}_X(\alpha_i), \widehat{q}_Y(\alpha_i) ) \in \mathbb{R}^2 : \alpha_i = \frac{i}{k} \textrm{, para }i\in\{1,2,\cdots,k-1\} \right\}, \end{equation*}\]

para natural $k \gt 2$. Estamos andando na curva anterior dando passos de tamanho $1/k$ no parâmetro $\alpha$. Por exemplo, para $k=10$, então plotamos $9$ os pontos referentes aos $\alpha_i$-quantis para $\alpha_i$$=0.1$, $0.2$, $\cdots$, $0.8$, $0.9$. Se temos $k=0.5$, então pegamos os $19$ pontos identificados por $\alpha_i$$=0.05$, $0.1$, $\cdots$, $0.9$, $0.95$.

Na Figura 4 temos vários QQ-plots para diferentes escolhas de variáveis aleatórias $X$ e $Y$, tamanhos das amostras $N$ e $M$, e números de pontos do plot $k-1$.

  • Na primeira imagem da Figura 4, temos que $X,Y\sim\mathcal{N}(0.5,1)$ com $N,M=200$ e $k=10$. Vemos que os pontos se aproximam da identidade, mas há uma pequena variação porque como a amostra é pequena as estimativas para os $\alpha$-quantis variam bastante.

  • Na segunda imagem, temos as mesmas distribuições, mas agora como $N,M=10000$ e $k=25$. Os $\alpha$-quantis estimados são mais precisos e por isso os pontos estão bem em cima da reta identidade.

  • Na terceira gravura, temos $X\sim\textrm{Uniforme}([0,1])$ e $Y\sim\mathcal{N}(0,1)$ com $N=2000$, $M=1000$ e $k=25$. Este é um caso em que a média das duas distribuições geradoras é igual (por isso os pontos do meio ficam próximos à identidade), mas conseguimos identificar a diferença das distribuições.

  • No caso da quarta imagem, temos $X\sim\mathcal{N}(0,1)$ e $Y\sim\mathcal{N}(1,1)$ com $N,M=3000$ e $k=20$. Como a distribuição é igual a menos da média, podemos perceber que os pontos fica na reta $y=x+1$ ao invés da identidade.

  • A quinta imagem é a versão amostral do QQ-plot que fizemos analiticamente anteriormente na Figura 2, quando temos $X\sim\textrm{Exp}(1)$ e $Y\sim\textrm{Uniforme}([0,1])$. Estamos fazenddo $N,M=2000$ e $k=100$.

  • Por fim, na última gravura temos um exemplo para comparação da distribuição binomial com a distribuição normal. Fazemos $X\sim\textrm{Binomial}(400,0.5)$ e $\mathcal{N}(200,100)$, como $N,M=4000$ e $k=20$.

    $\oint$ Para cada $t\in\mathbb{N^*}$, definindo $Z_t\sim\textrm{Binomial}(t,0.5)$, então temos que

    \[\frac{Z_t- 0.5\, t}{0.5\, \sqrt{t}}\overset{\mathscr{D}}{\to} \mathcal{N}(0,1)\]

    utilizando o teorema do limite central observando que $Z_t\sim\sum_{i=1}^t B_i$ em que $B_i \sim \textrm{Bernoulli}(0.5)$ são idependentes.

Figura 4: show me love

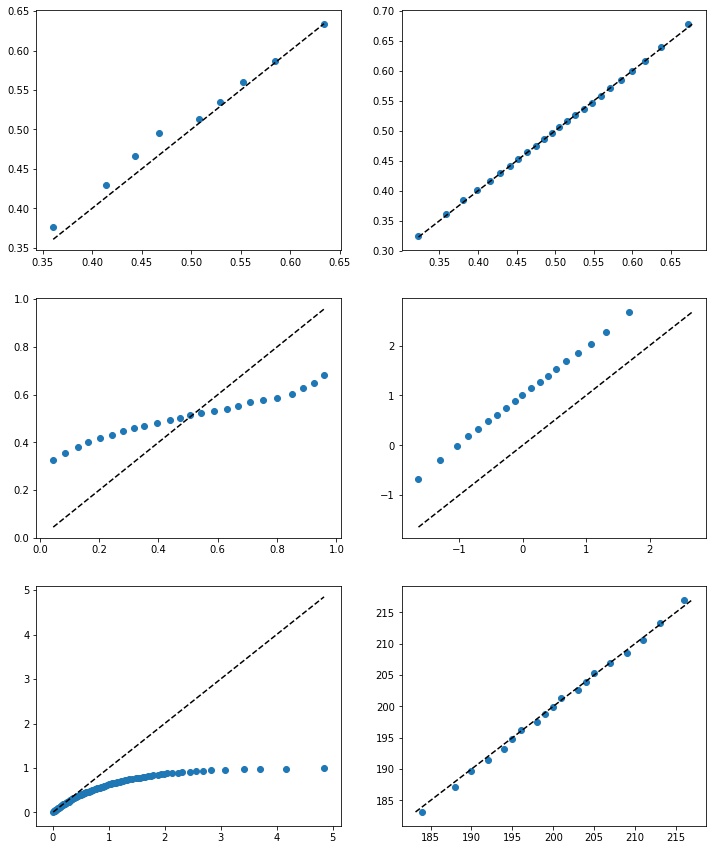
O QQ-plot foi construído originalmente para ser uma forma visual de identificar se duas amostras analisadas são de distribuições próximas ou não. A princípio, essa maneira de análise não nos dá uma métrica numérica que podemos estudar.

Sugestão de métrica quantitativa

Para obter um um valor numérico para que possamos avaliar se nossas distribuições estão próximas, devemos relembrar qual foi a motivação do QQ-plot: estamos comparação os pontos com a reta identidade. Isso nos leva a pensar em usar uma métrica de regressão do quão boa a reta identidade $f(x)=x$ se adapta aos nossos dados

\[\begin{equation*} \left\{ (\widehat{q}_X(\alpha_i), \widehat{q}_Y(\alpha_i) ) \in \mathbb{R}^2 : \alpha_i = \frac{i}{k} \textrm{, para }i\in\{1,2,\cdots,k-1\} \right\}. \end{equation*}\]

Utilizando o $\textrm{MSE}$ ou $\textrm{MAE}$, por exemplo, ficando com as expressões:

\[\begin{align} \textrm{MSE} = \frac{1}{k-1} \sum_{i=1}^{k-1} (f(\widehat{q}_Y(\alpha_i)) - \widehat{q}_Y(\alpha_i))^2 &= \frac{1}{k-1} \sum_{i=1}^{k-1} (\widehat{q}_X(\alpha_i) - \widehat{q}_Y(\alpha_i))^2 \textrm{,}\\ \textrm{e }\textrm{MAE} &= \frac{1}{k-1}\sum_{i=1}^{k-1} \left|\widehat{q}_X(\alpha_i) - \widehat{q}_Y(\alpha_i)\right|. \end{align}\]

$\oint$ Gosto da ideia de usar métricas como $\textrm{MSE}$ e $\textrm{MAE}$ pela simetria. Não importaria se trocássemos as amostras $X$ e $Y$ de lugar.

Na Figura 5 temos alguns exemplos de QQ-plots e suas respectivas métricas. Estamos usando sempre $N,M=3000$. Na primeira imagem temos $X, Y\sim\mathcal{N}(0,1)$, para $k=10$. Na segunda temos $X\sim\textrm{Uniforme}([0,1])$ e $Y\sim\textrm{Uniforme}([-1,2])$, para $k=25$. Na terceira imagem temos $X\sim\textrm{Uniforme}([0,1])$ e $Y\sim\mathcal{N}(0.5,1)$, com $k=30$. Por fim, temos $X,Y\sim\mathcal{N}(300,400)$, escolhendo $k=20$.

Figura 5: show me love

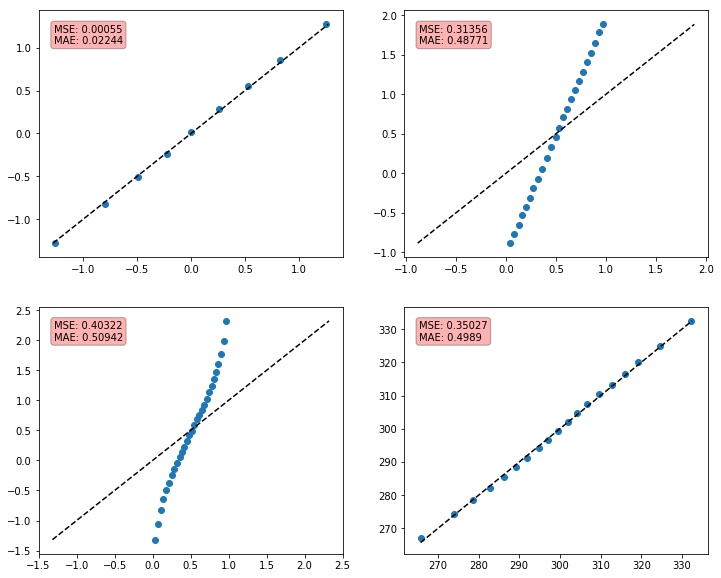
Como podemos ver, essa forma de cálculo das métricas não soluciona o problema. Dependendo da escala dos nossos dados podemos ter a métrica inflada, mesmo com as amostras vindo da mesma distribuição. Isso ocorre no último QQ-plot da Figura 5.

Uma sugestão pra manter os dados não muito maiores que $1$ em módulo é aplicar um StandardScaler nos nossos dados. Calculamos a média e variância amostral da amostra $\{x_1,x_2,\cdots,x_n\}$ e transformamos nossos dados de forma que agora

\[\begin{equation*} \left\{ x_i^* = \frac{x_i - \widehat{\mu_X}}{S^2_X}\right\} \textrm{, e também } \left\{ y_i^* = \frac{y_i - \widehat{\mu_X}}{S^2_X}\right\}. \end{equation*}\]

É importante notar que não estamos modificando o formato do QQ-plot, apenas deformando e transladando os eixos já que aplicamos o mesmo scaler nos dois eixos. A ideia é que se $X\sim Y$, então o scaller fitado na amostra de $X$ deveria deixar as duas amostras com média $0$ e variância $1$.

Na Figura 6 temos o QQ-plot utilizando essa metodologia e suas respectivas métricas. Agora, fixamos que $N,M=3000$ e $k=20$. Na primeira imagem temos $X\sim\textrm{Exp}(1)$ enquanto $Y\sim \mathcal{N}(0,1)$. Na segunda temos $X\sim \mathcal{N}(10,9)$ e $Y\sim\mathcal{N}(5,1)$. Na terceira imagem temos $X\sim \mathcal{N}(11,1)$ e $Y\sim \mathcal{N}(10,1)$. Por fim, na última temos $X,Y\sim \mathcal{N}(300,400)$.

Figura 6: show me love

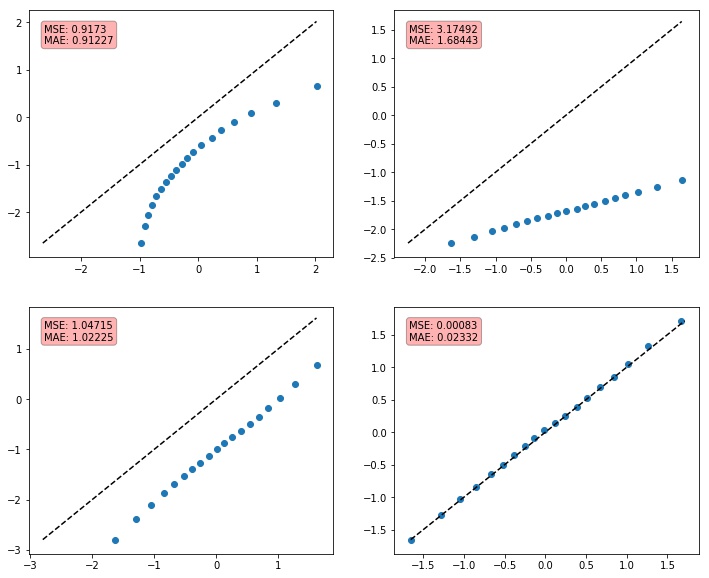
Com isso, temos maior esperança de ter métricas com valores baixos para amostras de uma mesma distribuição, independentes da escala, como é o caso da última imagem da Figura 6.

$\oint$ Um pequeno detalhe é que agora nem sempre temos a métrica simétrica, pois a média e variância da amostra de $Y$ possivelmente é diferente da de $X$.

Fixados $N$, $M$ e $k$, o ideal seria definir um $\varepsilon\in \mathbb{R}^+$ universal para criar um critério do tipo: se $ \textrm{MSE}$ (ou $\textrm{MAE}$) $< \varepsilon$, então desconfiamos que $X\sim Y$ e caso contrário, acreditamos que $X\nsim Y$. Entretanto essa tarefa parece impossível e o valor de $\varepsilon$ depende da natureza dos nossos dados e do quanto somos tolerantes com o problema de covariate shift.

Para avaliar se essa forma de monitoramento é útil, vale aplicar em alguns dados reais da área que você está analisando. Entender como se comportam as métricas sugeridas ($\textrm{MAE}$ e $\textrm{MSE}$) nos casos em que não há dataset shift e nos casos em que há.

Se você não tem muitas versões de tempos diferentes, ou se você não sabe se há ou não covariate shift, vale a pena dividir seus dados de uma mesma base em dois conjuntos disjuntos. Entender como fica a métrica aplicada a essas duas amostras e depois mudar artificialmente a distribuição da segunda somando e multiplicando ruídos aos dados.

Problemas e considerações finais

O QQ-plot é uma estratégia visual muito útil de verificação de covariate shift. É uma maneira interessante e eficiente de gerar relatórios de acompanhamento de qualidade de bases. Fácil de explicar e de implementar, não sendo muito custoso computacionalmente por apenas precisar ordenar os dados nos cálculos do $\alpha$-quantis. Apesar de suas qualidades, temos alguns problemas importantes.

O QQ-plot funciona bem para variáveis aleatórias contínuas. Porém, no geral, para variáveis aleatórias discretas temos funções quantis patológicas, com descontinuidades e as funções quantis estimadas não são muito confiáveis.

$\oint$ Imagine o cenário em que $X,Y\sim\textrm{Ber}(0.5)$, então podemos calcular $q_X(0.5)=0$. Mas agora, nas nossas amostras, temos uma com um valor de $0$ a mais e a outra um valor de $1$ a mais. Nesse cenário, as medianas estimadas seriam $0$ e $1$, respectivamente e ganharíamos um ponto completamente distante da nossa reta identidade. Esse problema independe do tamanhos das amostras e pode ocorrer inflando nossa métrica. A falta de continuidade gera esses problemas.

Além disso, com as variáveis aleatórias contínuas, o QQ-plot peca em não nos dar uma métrica numérica para avaliar em monitoramentos automatizados. A escolha de $\varepsilon$ é arbitrária demais e em muitos casos podemos gerar alertas desnecessários sendo muito rigorosos ou deixar passar casos problemáticos se formos muito tolerantes.

Por fim, esse tipo de métrica avalia nossas variáveis aleatórias de forma independentes. Em muitos casos, o covariate shift pode ocorrer na distribuição conjunta do vetor aleatório e não perceberemos isso olhando para as distribuições marginais. Um exemplo desse problema pode ser visto na Figura 7.

Figura 7: show me love

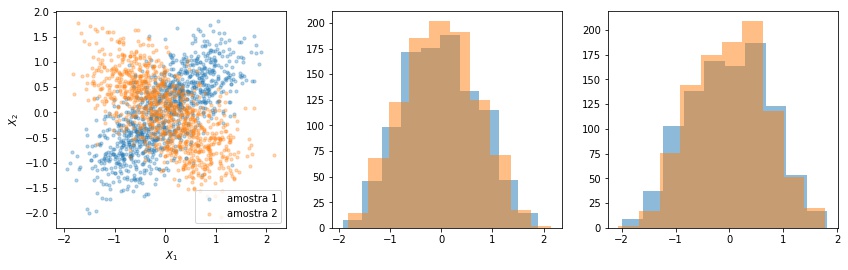
Nos próximos posts dessa série, vamos ver uma outra técnica que pode ajudar nesses casos. No geral, as técnicas de monitoramento de covariate shift tem seus pontos fortes e fracos. O ideal é sempre ter várias formas diferentes para identificar possíveis problemas e fazer intervenções.

Ajustar pequeno problema na equação com o align das metricas MAE MSE