Se fixarmos o poder preditivo no conjunto de desenvolvimento, um modelo com menos atributos tende a ter menor propensão de abusar de ruídos e relações espúrias do seu conjunto de treinamento, o que pode levá-lo a ganhos de performance fora do laboratório. Uma seleção bem feita de variáveis é, portanto, uma ferramenta data-centric importante na modelagem de problemas de aprendizado de máquina supervisionado.
$\oint$ Para ilustrar a afirmação anterior, temos, como exemplo, que a dimensão-VC (medida de complexidade de uma família de hipóteses) de um perceptron (classificador linear) é $d+1$, em que $d$ é o número de variáveis utilizadas no modelo [1]. Um modelo com dimensão-VC maior significa que você precisa de um volume de dados maior para garantir que sua performance, medida no treinamento, seja semelhante à performance real. Na prática, isso significa que quanto maior a dimensão-VC, maior a chance de overfitting. Consequentemente, nesse exemplo, se temos dois perceptrons com performances semelhantes no treino, com a diferença de que um tem mais variáveis que o outro, o que tem mais variáveis tem maior chance de apresentar overfitting [1].
Entretanto, a seleção de variáveis não é vista com o cuidado devido na maioria dos cursos de Aprendizado de Máquina. São apresentados poucos métodos e de maneira superficial. Os poucos lugares que discutem o tema, no geral, focam ainda em técnicas que são pouco escaláveis com o aumento de variáveis e, por isso, são pouco praticáveis na maioria das aplicações do mercado (como as estratégias gulosas de
sklearn.feature_selection.SequentialFeatureSelector).No DataLab da Serasa Experian, seleção de variáveis se torna extremamente relevante pela natureza dos problemas que trabalhamos. Na grande maioria dos casos temos algumas milhares de variáveis disponíveis no bureau de dados da Serasa e não é fácil identificar de antemão quais serão as features que nos darão mais ganhos. É necessário aplicar técnicas que são robustas à grandeza do número de variáveis que temos ao mesmo tempo que garantam uma seleção que faça sentido.
Neste post, iremos motivar a construção do Boruta [2], uma das técnicas mais utilizadas pelos cientistas do DataLab na seleção de features, com algumas dicas de uso prático. Ilustraremos ainda o uso da função
boruta.BorutaPy, do ambiente scikit-learn-contrib (ou seja, compatível com bibliotecas que seguem o padrão de código do scikit-learn).Para ilustrar o problema de seleção de features, utilizaremos o
sklearn.datasets.make_classification para criar um problema genérico de classificação em que podemos definir, como um parâmetro da função, o número de variáveis úteis para o problema de previsão.from sklearn.datasets import make_classification
N_FEATURES = 20
X, y = \
make_classification(n_samples=1000,
n_features=N_FEATURES,
n_informative=2,
n_redundant=2,
n_classes=2,
flip_y=0.1,
shuffle=False,
random_state=42)
X = pd.DataFrame(X, columns=[f'column_{i+1}' for i in range(N_FEATURES)])
X.head()
Como estamos escolhendo 2 features informativas e 2 features redundantes, temos que as 4 features mais importantes são as colunas:
column_1, column_2, column_3 e column_4.Motivando a construção do Boruta
Medindo a importância de uma variável
Uma das técnicas mais comuns para selecionar as variáveis é aproveitar-se de modelos que, de alguma forma, selecionam-nas no próprio processo de treinamento. Árvores e, consequentemente, comitês de árvores são, talvez, o melhor exemplo disso: pela estratégia gulosa de fazer a melhor quebra possível naquele instante (de acordo com algum critério de melhor, usualmente relacionado à pureza das folhas criadas, no caso de classificação), estamos sempre escolhendo variáveis relevantes. Variáveis pouco discriminativas são utilizadas muito menos que as variáveis que de fato ajudam a fazer a previsão [3].
Esse processo, naturalmente deriva medidas de importância para as variáveis como: o número de vezes que ela é utilizada (esse é o modo default do atributo
.feature_importance_ dos ensembles do LGBM, como o lightgbm.LGBMClassifier) ou uma ponderação do ganho de informação durante a escolha das quebras das features (essa é a forma default dos ensembles de árvores do sklearn, como o sklearn.ensemble.RandomForestClassifier, o sklearn.ensemble.ExtraTreesClassifier, e o sklearn.ensemble.HistGradientBoostingClassifier, além de também virar o atributo do LGBM quando definimos o importance_type='gain').Com alguma dessas medidas naturais de importância, é razoável ordenar nossas variáveis da mais importante para a menos importante.
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier(random_state=42).fit(X, y)
df_imp = \
(pd.DataFrame(list(zip(X.columns, rfc.feature_importances_)),
columns=['feature_name', 'feature_importance'])
.sort_values(by='feature_importance', ascending=False)
.reset_index(drop=True)
)
df_imp
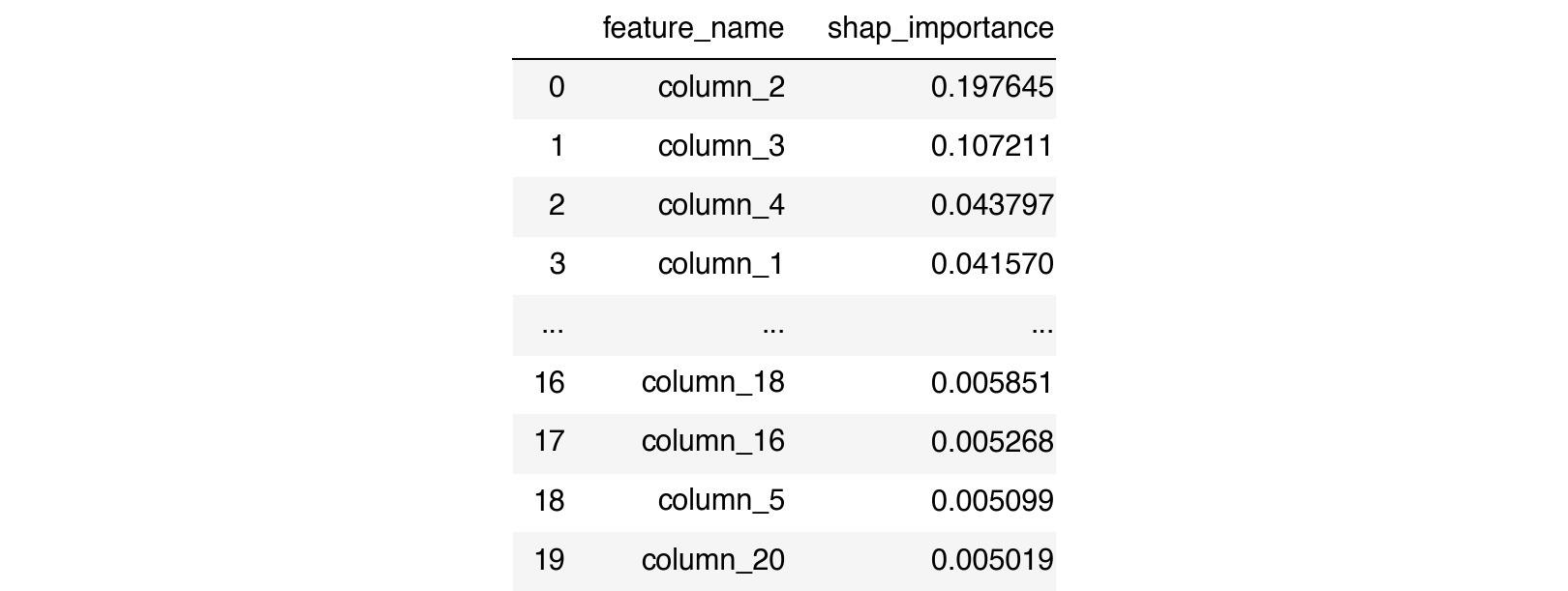
$\oint$ Existem algumas outras formas de metrificar a importância de uma variável como, por exemplo, utilizando suas contribuições de valores SHAP. Tendo em vista que o
shap.Explainer(model).shap_values(X) nos retorna uma medida de quanto aquela variável agregou na previsão, pegar a sua média entre todos os exemplos nos dá uma forma de ver o quão útil ela foi para discriminar os exemplos como um todo. Para os valores não se cancelarem (imagine uma variável que para determinados valores joga a previsão para cima e em outros valores joga a previsão para baixo), tomamos o módulo antes de fazer a média. Repare que a ordem das importâncias dada pelo SHAP pode ser diferente da ordem de importâncias dada pelo atributo de .feature_importance_ usual do estimador, como é o caso do nosso exemplo.explainer = shap.TreeExplainer(rfc)
shap_vals = explainer.shap_values(X)
df_imp_shap = \
(pd.DataFrame(list(zip(X.columns, np.abs(shap_vals[0]).mean(axis=0))),
columns=['feature_name', 'shap_importance'])
.sort_values(by='shap_importance', ascending=False)
.reset_index(drop=True)
)
df_imp_shap
Ainda não falamos do Boruta, mas ele se utiliza dessa ordenação para fazer suas análises e é implementado, usualmente, utilizando medida de importância do estimador (o atributo
.feature_importances_ ou .coef_ para algoritmos lineares). Essa diferença motivou alguns contribuidores a implementar o Boruta-Shap. Entretanto, incorporar o SHAP ao processo do Boruta não parece trivial e a biblioteca costuma ser lenta.Uma possível alternativa pode ser adaptar na mão o atributo
.feature_importance_ do seu classificador, salvando o X no momento de treinamento para utilização no cálculo do SHAP. Como implemento aqui:class SHAPImportanceRandomForestClassifier(RandomForestClassifier):
def fit(self, X, y, sample_weight=None):
self.X_ = X
super().fit(X, y, sample_weight=sample_weight)
return self
@property
def feature_importances_(self):
check_is_fitted(self)
explainer = shap.TreeExplainer(self)
shap_vals = explainer.shap_values(self.X_)
return np.abs(shap_vals[0]).mean(axis=0)
from shap_feature_importances_ import SHAPImportanceRandomForestClassifier
rfc_shap = SHAPImportanceRandomForestClassifier(random_state=42).fit(X, y)
rfc_shap.feature_importances_
array([0.04156985, 0.19764501, 0.10721142, 0.04379691, 0.00509938,
0.00967927, 0.00900892, 0.00769202, 0.01053711, 0.00973848,
0.00764462, 0.00725161, 0.00690175, 0.00718789, 0.00600269,
0.00526766, 0.00659648, 0.00585107, 0.00726538, 0.00501896])
Note que essa implementação utiliza o mesmo conjunto de treino para cálculo do SHAP. Existe algum debate aqui, mas tenha em mente que os valores de importância calculados com SHAP (média do valor absoluto) no teste podem ser diferentes dos valores de importância calculados com SHAP no treino. Se você quiser esse nível de preciosismo, pode estar interessado em reservar um pedaço do seu conjunto de dados para calcular os valores SHAP. Implemento essa ideia na classe
XSHAPImportanceRandomForestClassifier do arquivo shap_feature_importances_.py no repositório deste post. Entretanto, para poder dormir tranquilo, tenha em mente que o .feature_importances_ usual dos algoritmos baseados em árvore é calculado com o conjunto de treino, então calcular o SHAP no treino não é uma blasfêmia tão grande.Selecionando as K “melhores variáveis”
Se quisermos que nosso modelo tenha apenas as
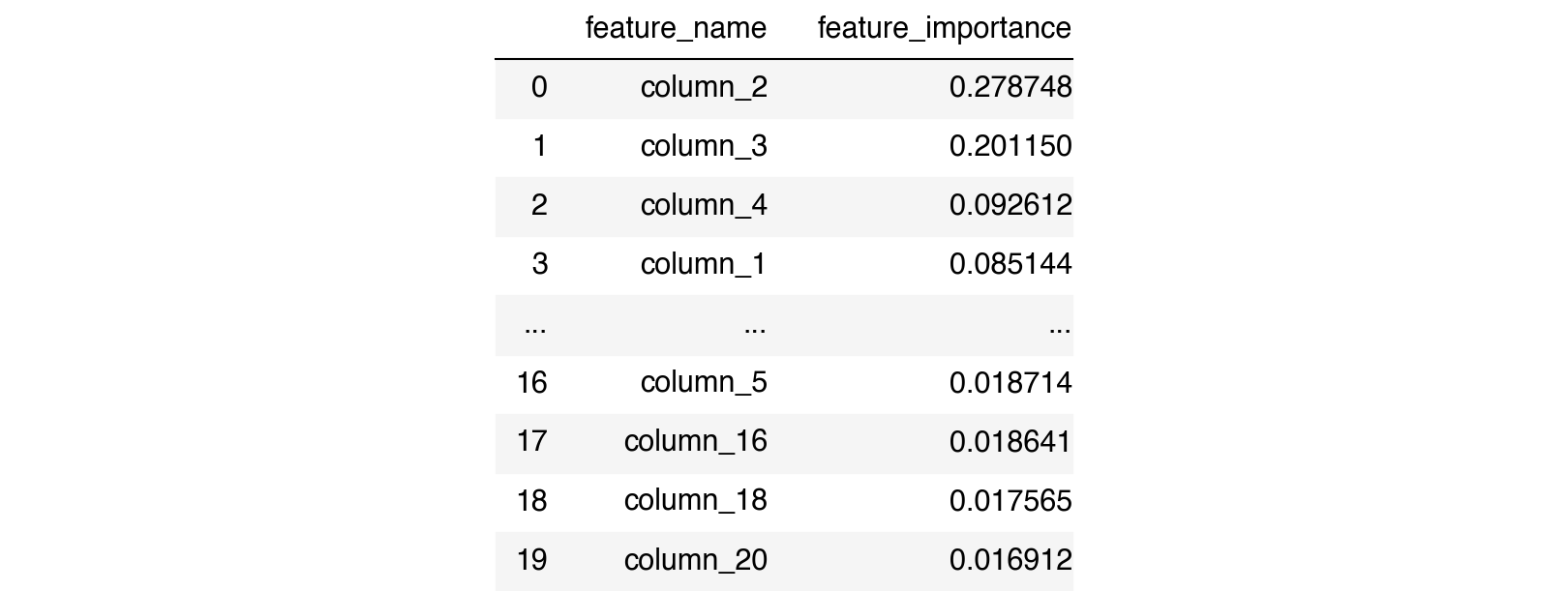
K features mais úteis, a maneira natural de escolher elas seria pegar as K variáveis com maiores valores de importância.K = 4
(df_imp
.head(K)
.feature_name
.to_list()
)
['column_2', 'column_3', 'column_4', 'column_1']
Essa é uma das estratégias mais comuns de se fazer seleção de features no mercado, mas levanta algumas questões. A primeira e mais imediata é: como escolher o número de variáveis
K ideal. Nesse caso ilustrativo, sabemos que 4 variáveis é o número correto, mas na maioria dos casos de aplicação real é irrealista ter esse número de antemão.$\oint$ Uma estratégia muito utilizada, mas que não vamos focar muito, é aumentar a lista de features do modelo seguindo a ordenação dada pelo modelo treinado em todas as features, encarando esse valor
K como um hiper-parâmetro que estamos otimizando. No exemplo abaixo, fazemos isso utilizando o sklearn.model_selection.GridSearchCV ao construir uma classe SelectKTop utilizando o padrão necessário para os selecionadores de variáveis do scikit-learn, isto é, seguindo a forma que o sklearn.feature_selection.SelectorMixin exige. Você pode ver a implementação dessa classe no arquivo selectktop_selector.py no repositório deste post.PS: A classe
SelectKTop é mais ou menos equivalente à classe sklearn.feature_selection.SelectFromModel, cuja existência descobri após terminar de escrever o post!from selectktop_selector import SelectKTop
from sklearn.model_selection import GridSearchCV, RepeatedStratifiedKFold
from sklearn.pipeline import make_pipeline
grid = (
GridSearchCV(
make_pipeline(SelectKTop(random_state=42),
RandomForestClassifier(random_state=42)),
param_grid={'selectktop__K': np.arange(1,N_FEATURES+1)},
cv=RepeatedStratifiedKFold(n_splits=5, n_repeats=3, random_state=42),
scoring='roc_auc')
.fit(X, y))
df_cv = (
pd.DataFrame(grid.cv_results_)[[
'param_selectktop__K',
'mean_test_score',
'std_test_score'
]])
cv_best = (
df_cv
.sort_values(by='mean_test_score', ascending=False)
.reset_index(drop=True)
.loc[0])
plt.errorbar(df_cv.param_selectktop__K, df_cv.mean_test_score, 1.96*df_cv.std_test_score)
plt.scatter(cv_best.param_selectktop__K, cv_best.mean_test_score, s=100)
plt.ylim(0.75, 1)
plt.xlabel('K of SelectKTop')
plt.xticks(df_cv.param_selectktop__K.astype(int))
plt.ylabel('Performance (ROCAUC)')
plt.show()
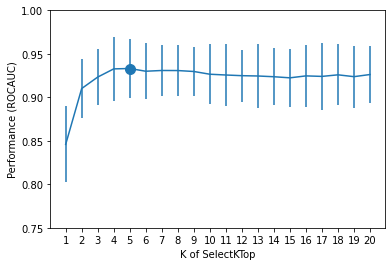
No nosso experimento controlado, encontramos algumas poucas variáveis a mais do que o correto (e ficamos com todas as úteis).
grid.best_estimator_.steps[0][1].get_feature_names_out()
array(['column_1', 'column_2', 'column_3', 'column_4', 'column_10'],
dtype=object)
Vale citar que podemos deixar esse método mais robusto variando o
random_state do base_estimator e tendo uma distribuição de importâncias para cada variável ao invés de apenas um valor único (que naturalmente é mais ruidoso). Utilizar essa técnica com o SHAP para medir a importância (passando por exemplo o SHAPImportanceRandomForestClassifier como base_estimator do SelectKTop) é algo muito utilizado por alguns cientistas do DataLab como alternativa ao Boruta que, como vamos ver, costuma ser muito demorado.Selecionando as K melhores variáveis com ponto de corte sugerido por uma variável aleatória
Criar uma variável de ruído, ou seja, que sabidamente não é útil para a previsão, nos auxilia a ter um ponto de corte para filtro das variáveis que demonstram ajudar na previsão. A ideia dessa abordagem é medir a importância da variável aleatória e ficar apenas com variáveis que se demonstrarem mais importantes do que ela.
Adicionando a nova coluna, por exemplo, amostrada de uma variável aleatória $\mathcal{N}(0,1)$ de forma independente, temos uma nova lista de importância das variáveis.
normal_noise_X = (X.assign(noise_column = np.random.RandomState(42).normal(size=X.shape[0])))
normal_noise_X[normal_noise_X.columns[::-1]].head()
normal_noise_rfc = RandomForestClassifier(random_state=42).fit(normal_noise_X, y)
df_imp_normal_noise = \
(pd.DataFrame(list(zip(normal_noise_X.columns, normal_noise_rfc.feature_importances_)),
columns=['feature_name', 'feature_importance'])
.sort_values(by='feature_importance', ascending=False)
)
df_imp_normal_noise
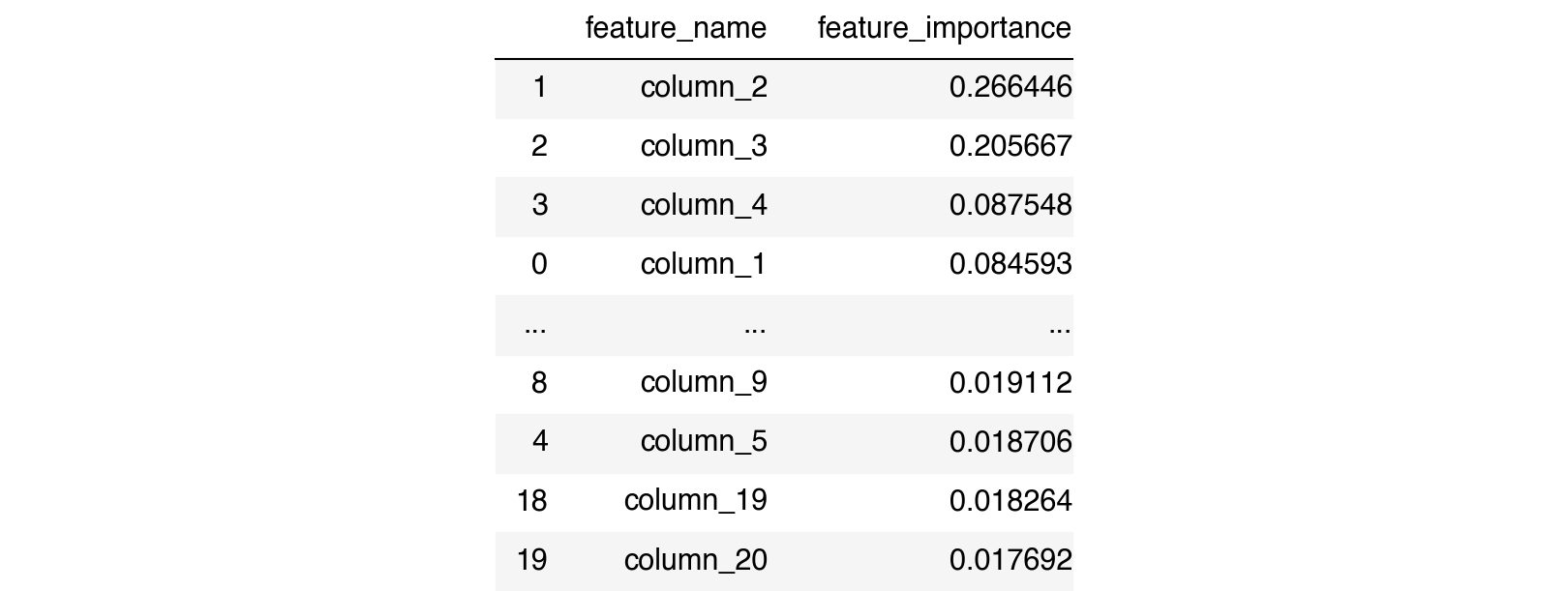
Como a última variável é a nossa coluna sabidamente ruidosa, a ideia dessa técnica é selecionar apenas as variáveis que têm importância maior do que o limiar definido pela importância da variável não relacionada.
normal_noise_importance = \
normal_noise_rfc.feature_importances_[-1]
np.array(
df_imp_normal_noise
.query(f"feature_importance > {normal_noise_importance}")
.feature_name
)
array(['column_2', 'column_3', 'column_4', 'column_1', 'column_6',
'column_10', 'column_14'], dtype=object)
Vale observar que, a escolha da variável ruidosa como $\mathcal{N}(0,1)$ foi totalmente arbitrária. Entretanto, isso faz diferença e pode fazer com que a seleção de variáveis seja distinta. No nosso exemplo controlado, mudar o ruído para $\textrm{Exp}(1)$ nos faria selecionar variáveis finais diferentes totalmente por sorte.
exp_noise_X = \
(X.assign(noise_column = np.random.RandomState(42).exponential(size=X.shape[0])))
exp_noise_rfc = \
RandomForestClassifier(random_state=0).fit(exp_noise_X, y)
exp_noise_importance = \
exp_noise_rfc.feature_importances_[-1]
np.array(
pd.DataFrame(list(zip(exp_noise_X.columns, exp_noise_rfc.feature_importances_)),
columns=['feature_name', 'feature_importance'])
.sort_values(by='feature_importance', ascending=False)
.query(f"feature_importance > {exp_noise_importance}")
.feature_name
)
array(['column_2', 'column_3', 'column_4', 'column_1', 'column_14',
'column_6', 'column_10', 'column_9', 'column_12', 'column_13',
'column_7', 'column_18'], dtype=object)
Isso nos demonstra um problema desse método. Apesar de poderoso, por nos dar um jeito interessante de selecionar as variáveis sem escolher
K de forma arbitrária, a escolha da distribuição da variável ruidosa é uma fonte de variação relevante.Em muitos casos, ter variáveis discretas versus contínuas pode influenciar na medida de importância (como é o caso de árvores que, por terem mais quebras disponíveis, terão mais chance de escolher uma variável ruidosa contínua) ou, ainda, a própria escala da feature adicionada pode atrapalhar nessa mensuração (por exemplo, se estamos usando os coeficientes angulares de um
sklearn.linear_model.Lasso).Toda essa variabilidade pode fazer com que, as vezes, uma feature ruim seja selecionada, ao passo que uma variável boa seja descartada por azar.
O Boruta vem para tentar lidar com essas duas questões ao mesmo tempo: tentar manter a distribuição marginal das features ruidosas iguais às distribuições marginais das features originais, enquanto tenta ser robusto à variabilidade, repetindo o experimento algumas vezes.
Ideias gerais do Boruta
Já existem muitos textos úteis que explicam o Boruta de forma didática e com exemplos. Como a ideia desse post não é ser redundante com a literatura e sim compilar ideias centrais de uso prático, vamos apenas citar os principais aspectos e deixar o convite para uma leitura detalhada de outras referências do tema como o post Boruta Explained Exactly How You Wished Someone Explained to You. A construção que fizemos anteriormente vai deixar as ideias do Boruta ainda mais claras, justificando o seu modo de ser.
Em resumo, o Boruta [2,4]:
- Cria variáveis não correlacionadas com a target ao embaralhar, entre as linhas, variáveis já presentes no dataset (essas são as variáveis que chamamos de shadow).
- Lida com a variabilidade repetindo o processo várias vezes e marcando quantas vezes a nossa variável de interesse ficou atrás do percentil
percdos.feature_importancesdas shadow features (por defaultperc=100, portanto, comparamos com o máximo dos.feature_importancesdas shadow features, isto é, se alguma shadow for melhor, já descartamos aquela variável de interesse naquela rodada). - Por fim, um teste de hipótese é feito para avaliar se podemos afirmar com alguma significância estatística
alphaque a feature de interesse é melhor que o percentilpercda importância das shadow features. - O teste de hipótese divide o conjunto de features em três categorias:
- As variáveis que estatisticamente são variáveis melhores que as shadow features (são as chamadas de
.support_); - As variáveis que estatisticamente são equivalentes às variáveis shadow (variáveis que excluímos);
- As variáveis que não são possíveis de afirmar com significância estatística como sendo melhores que as variáveis shadow (
.weak_support_).
- Na prática, a partir do momento que ele tem confiança de que uma determinada variável não é importante, ele já a exclui das próximas iterações.
O boruta.BorutaPy
Primeiro, precisamos instanciar um
base_estimator que será utilizado dentro do boruta.BorutaPy para calcular a importância das variáveis (através do .feature_importances_ ou do .coef_). É importante ressaltar que podemos adicionar hiper-parâmetros que acharmos relevantes para o problema, como o class_weight se temos um problema muito desbalanceado.Quando usamos um cômite de árvores, é importante ter em mente que árvores profundas vão mudar o
.feature_importances_, mas vão demorar mais para treinar. É justificável utilizar árvores mais rasas, uma vez que os ganhos mais expressivos são feitos nas primeiras quebras, usualmente.O
boruta.BorutaPy aceita qualquer estimador que tenha o atributo .feature_importances_ disponível após rodar o método .fit(X, y) [5]. Você pode utilizar isso a seu favor usando os estimadores mais adequados para o seu problema, inclusive, utilizando algoritmos baseados em árvores mais eficientes como as sklearn.ensemble.ExtraTreesClassifier (tenha em mente que as Extra Randomized Trees vão ter seu .feature_importances_ afetado pelo método de construção e isso pode impactar a escolha final de variáveis).Para exemplificar a utilização prática da biblioteca, vou utilizar o
SHAPImportanceRandomForestClassifier que criamos anteriormente (basicamente um sklearn.ensemble.RandomForestClassifier com SHAP no lugar do .feature_importances_ usual).from boruta import BorutaPy
boruta_forest = SHAPImportanceRandomForestClassifier(max_depth=7, random_state=42)
Um ponto de atenção que não é necessariamente claro na documentação, é que o parâmetro
n_estimators do boruta.BorutaPy sobrescreve o n_estimators do estimador como podemos ver no código fonte do BorutaPy:# set n_estimators
if self.n_estimators != 'auto':
self.estimator.set_params(n_estimators=self.n_estimators)
Por default, temos
n_estimators=1000. Se n_estimators='auto', então uma regra baseada no número de features que estamos avaliando é feita para escolher o número de árvores do ensemble.Por fim,
alpha e perc são os outros parâmetros importantes do boruta.BorutaPy que você deveria ficar atento:- O
perc(percentil do.feature_importances_das shadow features utilizado para decidir se as variáveis foram boas ou não naquela determinada rodada) é umintque vai de 0 a 100. Quanto mais próximo de 100, mais rigoroso estamos sendo na hora de avaliar nossas features. Pela aleatoriedade, alguns.feature_importances_de shadow features podem ser grandes e muito rigorosos com o critério de corte, nesse caso, isso será ruim porque estaremos excluindo variáveis marginais que são relevantes, mas não têm uma importância tão expressiva. O default desse parâmetro é 100, mas recomendo abaixá-lo levemente (para 90, por exemplo) caso esteja trabalhando com um problema com muitas variáveis, desse modo haverá maior chance de se ter uma shadow feature com importância alta. - O
alphaé um float que vai de 0 a 1 e é importante para delimitar a partição que fazemos do conjunto de variáveis (.support_weak_,.supporte excluídas), uma vez que determinará o rigor de certeza que queremos ter para afirmar que uma determinada feature é relevante ou não para o problema de classificação (ou regressão). O default desse parâmetro é 0.05, e eu não tenho o costume de alterá-lo, pois prefiro mantê-lo fixo e variar opercjá que os dois se relacionam.
boruta = \
(BorutaPy(
estimator=boruta_forest,
n_estimators=50,
max_iter=100, # number of trials to perform
random_state=42)
.fit(np.array(X), np.array(y)) # fit accepts np.array, not pd.DataFrame
)
Por fim, é fácil resgatar as features com os atributos
.support_ e .support_weak_.green_area = X.columns[boruta.support_].to_list()
blue_area = X.columns[boruta.support_weak_].to_list()
print('Support columns:', green_area)
print('Weak support columns:', blue_area)
Support columns: ['column_1', 'column_2', 'column_3', 'column_4', 'column_10']
Weak support columns: ['column_9']
Trade-off de “qualidade da seleção” vs “tempo” quando damos um undersample
Quando temos um dataset muito grande, o
boruta.BorutaPy pode demorar bastante tempo para rodar pelo processo de criar tantas variáveis shadows quanto temos no conjunto inicial de variáveis. Em muitas aplicações práticas é necessário aplicar o boruta.BorutaPy em um subconjunto do seu conjunto de treinamento.Faremos aqui um experimento para ver, em um caso sintético de
make_classification com n_samples=5000, n_features=100, n_informative=40 e n_redundant=10, como seriam as escolhas de variáveis de um boruta.BorutaPy conforme variamos o parâmetro frac de um .sample feito na base de desenvolvimento.from boruta_sample_experiment import experiment, plot_heatmap, plot_percentage_time
dic_sample, matrix, X_big, y_big = \
experiment(fracs=[0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1])
100%|██████████| 11/11 [14:08<00:00, 77.18s/it]
Como o número de variáveis informativas mais o número de variáveis redundantes é 50 então, nesse exemplo controlado, metade das nossas features são importantes. No plot abaixo, para diferentes valores de
frac (fração dos exemplos da base usado para treinar o boruta.BorutaPy) vemos quais variáveis estão sendo escolhidas. Idealmente, o boruta.BorutaPy deveria conseguir identificar que as primeiras 50 variáveis (eixo x) são as úteis e selecioná-las (pintando-as de verde), enquanto exclui as 50 demais (pintando-as de azul), haja vista que são ruído. Conforme variamos o frac (eixo y), vemos como ele se comporta.plot_heatmap(dic_sample, matrix)
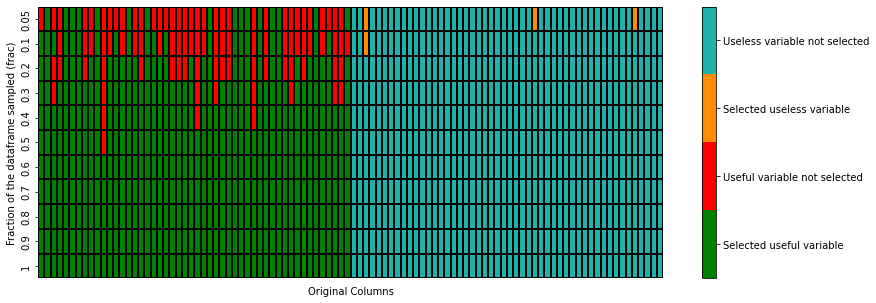
Na primeira figura abaixo, vemos uma sumarização do plot anterior variando o
frac (eixo x), enquanto observamos a porcentagem das variáveis úteis (em verde) e inúteis (em laranja) que são escolhidas. No gráfico ao lado, há uma análise de tempo (de treinamento do boruta.BorutaPy) e performance do modelo treinado com as variáveis escolhidas naquele valor de frac.plot_percentage_time(dic_sample, matrix, X_big, y_big)
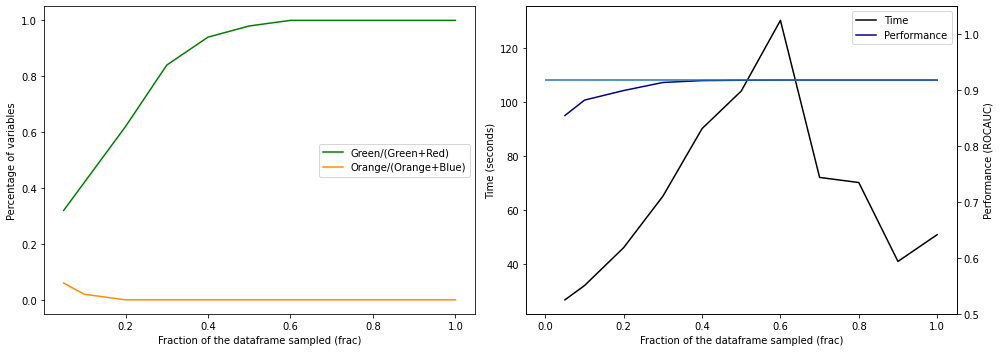
Como podemos ver, não precisamos de todas as amostras para treinar o nosso
boruta.BorutaPy. No exemplo anterior, apesar da nossa amostra ter 5000 elementos, com algo em torno de 3000 exemplos, já era possível encontrar perfeitamente todas as 50 variáveis úteis para o nosso problema.Na minha experiência utilizando o
boruta.BorutaPy, me sinto confortável com _uma amostra com 15 vezes mais exemplos do que features (ou seja, n_samples>=15*n_features)_. Nesse limiar, já costumo ter resultados bons em termos de seleção de variáveis e é possível rodar o algoritmo (em tempo satisfatório para desenvolvimento) com um max_depth controlado. Colocando um exemplo numérico: se, no DataLab, estou trabalhando com um problema de 5 mil variáveis, me sinto confortável em rodar o boruta.BorutaPy em uma amostra de 75 mil linhas, mesmo tendo muito mais exemplos na base de desenvolvimento.Por outro lado, o exemplo anterior nos mostra que nem sempre isso é o melhor, mesmo em questão de tempo. O
boruta.BorutaPy, na prática, não vai rodar por max_iter se já tiver certeza (no nível de significância alpha) das variáveis que ele acha úteis para o problema, que ele já exclui (ou seleciona) no meio do caminho. No experimento anterior, ter mais exemplos, na verdade, fez com que o boruta.BorutaPy ficasse com mais certeza de forma mais rápida sobre as variáveis. Na prática, isso dificilmente acontece.Usando o Boruta na prática e algumas alternativas
As ideias por trás do
boruta.BorutaPy são muito interessantes, mas o algoritmo final é temporalmente custoso. Por sorte, podemos utilizar as ideias da construção para fazer variações espertas que podem ser alternativas se uma rodada inicial (com max_depth ~ 10, perc=90 e n_estimators=500) estiver demorando demais:- Utilizar o
SelectKTopcom alguma métrica de.feature_importances_mais robusta (como o SHAP, usando algo como nossoSHAPImportanceRandomForestClassifier) e tendo cuidado com a escolha doK; - Adaptar o
SelectKTopque construímos para um versão ainda mais robusta que lida com uma distribuição de.feature_importances_ao invés de apenas um estimador (aliás, esse é um ótimo exercício para o leitor interessado em entender melhor a API do scikit-learn); - Adaptar o
SelectKToppara um "SelectAboveNoise", que explicamos anteriormente, criando as variáveis aleatórias a partir donumpy.random(outro exercício muito bom); - Utilizar o
boruta.BorutaPycom algoritmos mais rápidos (comosklearn.ensemble.ExtraTreesClassifier), mas lembrando que seu treinamento (ainda mais randomizado) vai afetar o.feature_importances_e, consequentemente, o resultado final. - Reduzir a amostra utilizada para treino do
boruta.BorutaPyrespeitando a rule of thumb den_samples>=15*n_features. - Mexer mais estruturalmente no algoritmo de forma que ele crie menos variáveis shadows em problemas com muitas variáveis (to be tested).
Se o seu problema é razoavelmente pequeno, usar o
boruta.BorutaPy com o SHAP e otimizar os hiper-parâmetros do boruta.BorutaPy é uma boa opção. Para isso, será útil utilizar o Boruta que criei no arquivo boruta_selector.py no repositório deste post. Ele já está no formato adequado de Selector do scikit-learn e pode ser utilizado da mesma forma que vimos o SelectKTop sendo usado (com um pipeline e qualquer BaseSearchCV do scikit-learn).Conclusão
Seleção de variáveis é um assunto necessário quando queremos garantir ter um modelo robusto. Neste post vimos uma das técnicas mais úteis para abordar esse problema enquanto, ao entender suas ideias, discutimos como adaptá-la para uma variedade de casos específicos. Mesmo que você não consiga usar o Boruta no seu problema em questão, as ideias aqui expostas permitem que você faça uma seleção de variáveis sabendo melhor as falhas e os benefícios de abordagens usuais do mercado.
Referências
[3] Decision and Classification Trees, Clearly Explained!!!. Josh Starmer. StatQuest with Josh Starmer.
Para mais dicas práticas de uso (e com um argumento de autoridade muito melhor que o meu), o autor do Boruta tem o guia Boruta for those in a hurry que, apesar de estar escrito em R, tem dicas práticas interessantes de alguém que conhece a implementação com muita profundidade.
Todos os arquivos e ambiente para reprodução dos experimentos podem ser encontrado no repositório deste post.
Este post foi originalmente publicado no Medium do Experian DataLab! Passe no post e deixe uma palminha, se achar que faz sentido! :D